SINUSOIDAL WAVES
If you ask someone to describe wave motion, they are likely to picture water waves and sketch a curve that looks like a sine wave. A sine wave represents just one of many possible shapes for a wave. But it is an important shape because it is often seen in nature and it is easy to handle mathematically. We will see shortly that any arbitrary wave shape can be constructed from sine waves, thus the sine wave can be thought of as a basic building block of wave motion.
To relate the mathematical sine function to wave motion, recall our definition of sine function shown back in Figure (1). The point of that figure is that the sine function is the sideways projection of circular motion. As the arrow rotates at an angular velocity ω, the angle θ that the arrow has rotated increases as θ = ωt . On the right we have graphed the height of the rotating arrow as a function of the angle θ = ωt to obtain a sine curve.
To actually create the sine wave shape seen in Figure (1), you can start shaking one end of a long rope as shown in Figure (2). If you move your hand up and
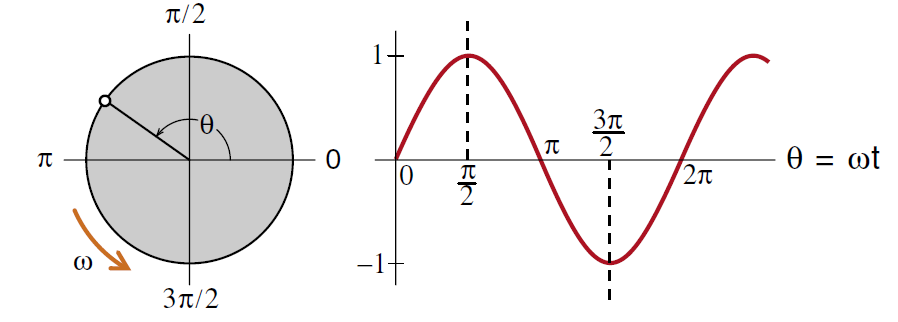
Figure 1: Definition of the function sin θ = sin(ω t).
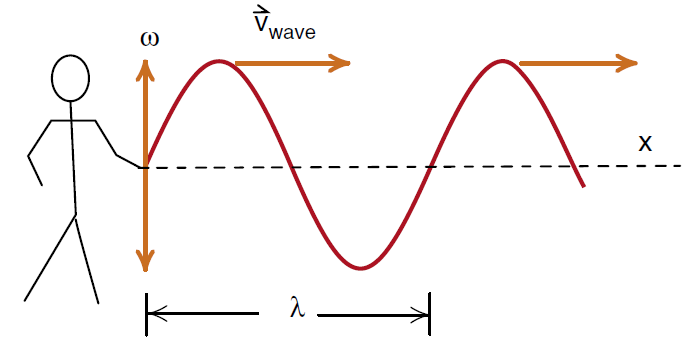
Figure 2: Sine wave created on a stretched rope.
down with a sinusoidal oscillation, a sinusoidal shaped wave will start traveling down the rope, at a speed 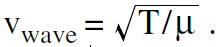 . This creates an example of what is called a traveling sine wave. The problem with creating traveling sine waves on a rope, is that the wave reaches the end of the rope, reflects, and moves back through the incoming wave, complicating the situation. A better example of traveling sine waves can be seen on the surface of a lake or the ocean where there is plenty of room for the waves to move before they strike an object or a shore.
. This creates an example of what is called a traveling sine wave. The problem with creating traveling sine waves on a rope, is that the wave reaches the end of the rope, reflects, and moves back through the incoming wave, complicating the situation. A better example of traveling sine waves can be seen on the surface of a lake or the ocean where there is plenty of room for the waves to move before they strike an object or a shore.
There are two distinct ways to view a traveling sine wave. One is to move along with the wave. Then all you see is a stationary sinusoidal shape. The other is to stand still and let the wave pass by you. Then you will see the wave oscillate up and down as successive crests and troughs pass by you. This is illustrated in Figure (3) where we have sketched a traveling sinusoidal water wave passing a fixed post in the water. If you move along with the wave, then the shape of the wave does not change. But if you look at the post, the level of the water is moving up and down with a sinusoidal oscillation.
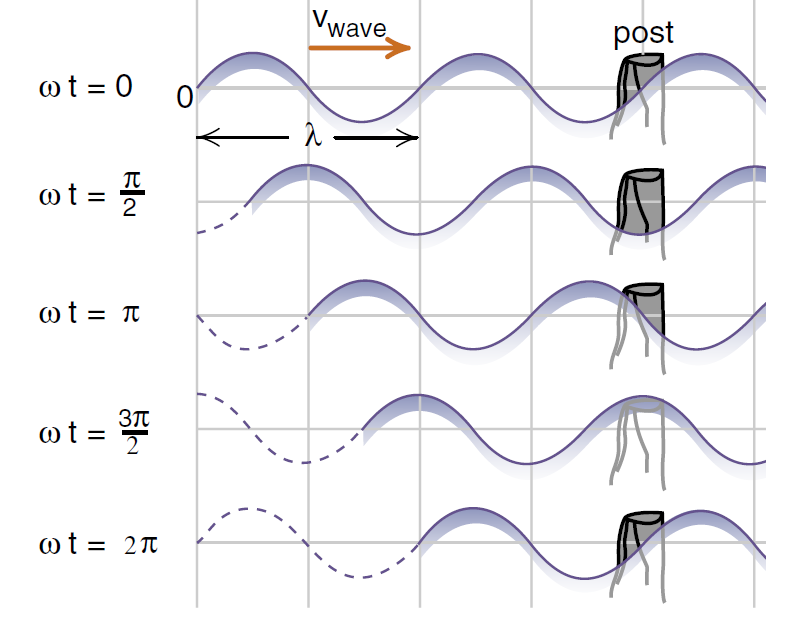
Figure 3: Traveling sine wave on the surface of water. The sine wave shape moves as a unit along the surface at a speed vwave . But if we look at a fixed post in the water, the water level at the post oscillates up and down with a sinusoidal oscillation.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


