

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Multiperfect Number
المؤلف:
Beck, W. and Najar, R.
المصدر:
"A Lower Bound for Odd Triperfects." Math. Comput. 38
الجزء والصفحة:
...
26-11-2020
2631
Multiperfect Number
A number 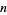 is
is 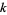 -multiperfect (also called a
-multiperfect (also called a 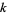 -multiply perfect number or
-multiply perfect number or 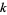 -pluperfect number) if
-pluperfect number) if
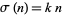 |
for some integer 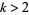 , where
, where 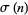 is the divisor function. The value of
is the divisor function. The value of 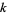 is called the class. The special case
is called the class. The special case 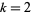 corresponds to perfect numbers
corresponds to perfect numbers 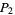 , which are intimately connected with Mersenne primes (OEIS A000396). The number 120 was long known to be 3-multiply perfect (
, which are intimately connected with Mersenne primes (OEIS A000396). The number 120 was long known to be 3-multiply perfect (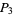 ) since
) since
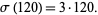 |
The following table gives the first few 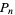 for
for 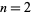 , 3, ..., 6.
, 3, ..., 6.
| 2 | A000396 | 6, 28, 496, 8128, ... |
| 3 | A005820 | 120, 672, 523776, 459818240, 1476304896, 51001180160 |
| 4 | A027687 | 30240, 32760, 2178540, 23569920, ... |
| 5 | A046060 | 14182439040, 31998395520, 518666803200, ... |
| 6 | A046061 | 154345556085770649600, 9186050031556349952000, ... |
Lehmer (1900-1901) proved that 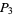 has at least three distinct prime factors,
has at least three distinct prime factors, 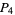 has at least four,
has at least four, 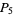 at least six,
at least six, 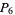 at least nine, and
at least nine, and 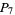 at least 14, etc.
at least 14, etc.
As of 1911, 251 pluperfect numbers were known (Carmichael and Mason 1911). As of 1929, 334 pluperfect numbers were known, many of them found by Poulet. Franqui and García (1953) found 63 additional ones (five 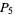 s, 29
s, 29 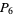 s, and 29
s, and 29 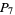 s), several of which were known to Poulet but had not been published, bringing the total to 397. Brown (1954) discovered 110 pluperfects, including 31 discovered but not published by Poulet and 25 previously published by Franqui and García (1953), for a total of 482. Franqui and García (1954) subsequently discovered 57 additional pluperfects (3
s), several of which were known to Poulet but had not been published, bringing the total to 397. Brown (1954) discovered 110 pluperfects, including 31 discovered but not published by Poulet and 25 previously published by Franqui and García (1953), for a total of 482. Franqui and García (1954) subsequently discovered 57 additional pluperfects (3 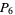 s, 52
s, 52 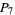 s, and 2
s, and 2 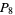 s), increasing the total known to 539.
s), increasing the total known to 539.
An outdated database is maintained by R. Schroeppel, who lists 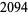 multiperfects, and up-to-date lists by J. L. Moxham and A. Flammenkamp. It is believed that all multiperfect numbers of index 3, 4, 5, 6, and 7 are known. The number of known
multiperfects, and up-to-date lists by J. L. Moxham and A. Flammenkamp. It is believed that all multiperfect numbers of index 3, 4, 5, 6, and 7 are known. The number of known 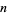 -multiperfect numbers are 1, 37, 6, 36, 65, 245, 516, 1134, 2036, 644, 1, 0, ... (Moxham 2001, Flammenkamp, Woltman 2000). Moxham (2000) found the largest known multiperfect number, approximately equal to
-multiperfect numbers are 1, 37, 6, 36, 65, 245, 516, 1134, 2036, 644, 1, 0, ... (Moxham 2001, Flammenkamp, Woltman 2000). Moxham (2000) found the largest known multiperfect number, approximately equal to 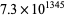 , on Feb. 13, 2000.
, on Feb. 13, 2000.
If 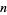 is a
is a 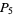 number such that
number such that 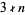 , then
, then 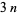 is a
is a 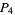 number. If
number. If 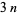 is a
is a 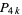 number such that
number such that 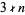 , then
, then 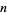 is a
is a 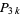 number. If
number. If 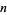 is a
is a 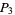 number such that 3 (but not 5 and 9) divides
number such that 3 (but not 5 and 9) divides 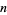 , then
, then 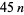 is a
is a 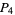 number.
number.
REFERENCES:
Beck, W. and Najar, R. "A Lower Bound for Odd Triperfects." Math. Comput. 38, 249-251, 1982.
Brown, A. L. "Multiperfect Numbers." Scripta Math. 20, 103-106, 1954.
Carmichael and Mason, T. E. Proc. Indian Acad. Sci., 257-270, 1911.
Cohen, G. L. and Hagis, P. Jr. "Results Concerning Odd Multiperfect Numbers." Bull. Malaysian Math. Soc. 8, 23-26, 1985.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 33-38, 2005.
Flammenkamp, A. "Multiply Perfect Numbers." https://www.uni-bielefeld.de/~achim/mpn.html.
Franqui, B. and García, M. "Some New Multiply Perfect Numbers." Amer. Math. Monthly 60, 459-462, 1953.
Franqui, B. and García, M. "57 New Multiply Perfect Numbers." Scripta Math. 20, 169-171, 1954.
Guy, R. K. "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 45-53, 1994.
Helenius, F. W. "Multiperfect Numbers (MPFNs)." https://home.netcom.com/~fredh/mpfn/.
Lehmer, D. N. Ann. Math. 2, 103-104, 1900-1901.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 149-151, 1979.
Moxham, J. L. "New Largest MPFN." mpfn@cs.arizona.edu posting, 13 Feb 2000.
Moxham, J. L. "1 New mpfns Total=4683." mpfn@cs.arizona.edu posting, 26 Mar 2001.
Perrier, J.-Y. "The Multi-Perfect Numbers." https://diwww.epfl.ch/~perrier/Multiparfaits.html
Poulet, P. La Chasse aux nombres, Vol. 1. Brussels, pp. 9-27, 1929.
Schroeppel, R. "Multiperfect Numbers-Multiply Perfect Numbers-Pluperfect Numbers-MPFNs." Rev. Dec. 13, 1995. ftp://ftp.cs.arizona.edu/xkernel/rcs/mpfn.html.
Schroeppel, R. (moderator). mpfn mailing list. e-mail rcs@cs.arizona.edu to subscribe.
Sloane, N. J. A. Sequences A000396/M4186, A005820/M5376, A027687, A046060, and A046061 in "The On-Line Encyclopedia of Integer Sequences."
Sorli, R. "Multiperfect Numbers." https://www-staff.maths.uts.edu.au/~rons/mpfn/mpfn.htm.
Woltman, G. "5 new MPFNs." mpfn@cs.arizona.edu posting, 23 Sep 2000.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















