المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Nonarithmetic Progression Sequence |
 1550
 02:47 صباحاً
date: 2-11-2020 |
Author : Allouche, J.-P. and Shallit, J. 
Book or Source : "The Ring of k-Regular Sequences." Theor. Comput. Sci. 98 
Page and Part : ...|
Read More
Date: 26-6-2020
852
Date: 24-12-2020
1128
Date: 1-8-2020
876
|
Given two starting numbers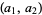 
, the following table gives the unique sequences 
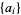that contain no three-term arithmetic progressions.
| Sloane | sequence |
| A003278 | 1, 2, 4, 5, 10, 11, 13, 14, 28, 29, 31, 32, ... |
| A033156 | 1, 3, 4, 6, 10, 12, 13, 15, 28, 30, 31, 33, ... |
| A033157 | 1, 4, 5, 8, 10, 13, 14, 17, 28, 31, 32, 35, ... |
| A033158 | 1, 5, 6, 8, 12, 13, 17, 24, 27, 32, 34, 38, ... |
| A033159 | 2, 3, 5, 6, 11, 12, 14, 15, 29, 30, 32, 33, ... |
| A033160 | 2, 4, 5, 7, 11, 13, 14, 16, 29, 31, 32, 34, ... |
| A033161 | 2, 5, 6, 9, 11, 14, 15, 18, 29, 32, 33, 36, ... |
| A033162 | 3, 4, 6, 7, 12, 13, 15, 16, 30, 31, 33, 34, ... |
| A033163 | 3, 5, 6, 8, 12, 14, 15, 17, 30, 32, 33, 35, ... |
| A033164 | 4, 5, 7, 8, 13, 14, 16, 17, 31, 32, 34, 35, ... |
REFERENCES:
Allouche, J.-P. and Shallit, J. "The Ring of k-Regular Sequences." Theor. Comput. Sci. 98, 163-197, 1992.
Erdős, P. and Turán, P. "On Some Sequences of Integers." J. London Math. Soc. 11, 261-264, 1936.
Gerver, J.; Propp, J.; and Simpson, J. "Greedily Partitioning the Natural Numbers into Sets Free of Arithmetic Progressions." Proc. Amer. Math. Soc. 102, 765-772, 1988.
Guy, R. K. "Theorem of van der Waerden, Szemerédi's Theorem. Partitioning the Integers into Classes; at Least One Contains an A.P." §E10 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 204-209, 1994.
Iacobescu, F. "Smarandache Partition Type and Other Sequences." Bull. Pure Appl. Sci. 16E, 237-240, 1997.
Ibstedt, H. "A Few Smarandache Sequences." Smarandache Notions J. 8, 170-183, 1997.
Sloane, N. J. A. Sequences A003278/M0975, A033156, A033157, A033158, A033159, A033160, A033161, A033162, A033163, and A033164 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|
