Lucas Chain

A Lucas chain for an integer 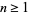 is an increasing sequence

of integers such that every 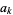, , 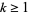can be written as a sum  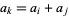of smaller elements whose difference  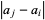is also en element of the sequence or zero (i.e., taking  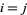is allowed). The number  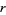is called the length of the chain.

For example, 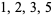 is a Lucas chain of length 3 for 5 because 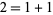, , 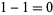, , 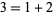, 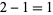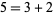and 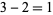. Further examples are sequences of consecutive powers of 2 or the Fibonacci numbers 1, 2, 3, 5, 8, 13, 21, ....

Lucas chains are a special kind of addition chain and can be used to evaluate Lucas functions, which have been proposed for use in public-key cryptography.

REFERENCES:

Kutz, M. "Lower Bounds for Lucas Chains." SIAM J. Comput. 31, 1896-1908, 2002.

Montgomery, P. L. "Evaluating Recurrences of Form 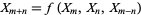 via Lucas Chains." Unpublished manuscript. ftp://ftp.cwi.nl:/pub/pmontgom/Lucas.ps.gz.

Yen, S.-M. and Laih, C.-S. "Fast Algorithms for LUC Digital Signature Computation." IEE Proc.--Computers and Digital Techn. 142, 165-169, Mar. 1995.