196-Algorithm
Take any positive integer of two digits or more, reverse the digits, and add to the original number. This is the operation of the reverse-then-add sequence. Now repeat the procedure with the sum so obtained until a palindromic number is obtained. This procedure quickly produces palindromic numbers for most integers. For example, starting with the number 5280 produces the sequence 5280, 6105, 11121, 23232. The end results of applying the algorithm to 1, 2, 3, ... are 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11, 33, 44, 55, 66, 77, 88, 99, 121, ... (OEIS A033865). The value for 89 is especially large, being 8813200023188.
The first few numbers not known to produce palindromes, sometimes known as Lychrel numbers (VanLandingham), are 196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, ... (OEIS A023108).
The numbers obtained by iteratively applying the algorithm to 196, the smallest such number, are 196, 887, 1675, 7436, 13783, ... (OEIS A006960), and no palindromic member of this sequence is known. The special number 196 therefore lends itself to the name of the reverse-then-add algorithm. In 1990, John Walker computed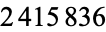 
iterations of the algorithm on 196 and obtained a number having 
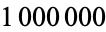digits. This was extended in 1995 by Tim Irvin, who obtained a number having 
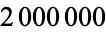digits. M. Sofroniou (pers. comm., Feb. 16, 2002) gave an efficient Wolfram Language implementation that has complexity 
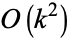for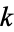 
steps, requiring approximately 10.6 hours on a 450 MHz Pentium II to compute 
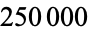iterations. Extrapolating the timing data suggests that approximately 42 days would be needed on this same machine to match Walker's 
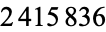iterations.
The rec.puzzles archive incorrectly states that a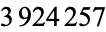 
-digit nonpalindromic number is obtained after 
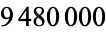iterations. However, the correct resulting number is 
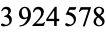digits long. As of May 1, 2006, it had been determined after 
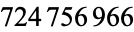iterations that a resulting palindromic number would have more than 300 million digits (VanLandingham).
The number of terms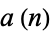 
in the iteration sequence required to produce a palindromic number from 
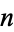(i.e., 
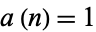for a palindromic number, 
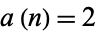if a palindromic number is produced after a single iteration of the 196-algorithm, etc.) for 
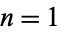, 2, ... are 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 3, 2, 2, 1, ... (OEIS A030547). The smallest numbers that require 
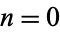, 1, 2, ... iterations to reach a palindrome are 0, 10, 19, 59, 69, 166, 79, 188, ... (OEIS A023109).
REFERENCES:
De Geest, P. "Websources about '196' Becoming Palindromic by Using Reversal Sums." https://www.worldofnumbers.com/weblinks.htm.
Eddins, S. "The Palindromic Order of a Number." IMSA Math. J. 4, Spring 1996. https://www.imsa.edu/edu/math/journal/volume4/webver/palinord.html.
Gardner, M. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, pp. 242-245, 1979.
Gruenberger, F. "How to Handle Numbers with Thousands of Digits, and Why One Might Want To." Sci. Amer. 250, 19-26, Apr. 1984.
Irving, T. "About Two Months of Computing, or, An Addendum to Mr. Walker's Three Years of Computing" https://www.fourmilab.ch/documents/threeyears/two_months_more.html.
Math Forum. "Ask Dr. Math: Making Numbers into Palindromic Numbers." https://mathforum.org/dr.math/problems/barnes10.11.html.
MathPages. "Digit Reversal Sums Leading to Palindromes." https://www.mathpages.com/home/kmath004.htm.
Peters, I. J. "Search for the Biggest Numeric Palindrome." https://www.floot.demon.co.uk/palindromes.html.
rec.puzzles archive. 1996. ftp://rtfm.mit.edu/pub/usenet/news.answers/puzzles/archive/arithmetic/part1.
Sloane, N. J. A. Sequences A006960/M5410, A023108, A023109, A030547, and A033865 in "The On-Line Encyclopedia of Integer Sequences."
VanLandingham, W. "196 and Other Lychrel Numbers." https://www.p196.org/.
Walker, J. "Three Years of Computing: Final Report on the Palindrome Quest." https://www.fourmilab.ch/documents/threeyears/threeyears.html.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
