تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Tribonacci Number
المؤلف:
Dumitriu, I.
المصدر:
"On Generalized Tribonacci Sequences and Additive Partitions." Disc. Math. 219
الجزء والصفحة:
...
30-9-2020
1386
+
-
20
Tribonacci Number
The tribonacci numbers are a generalization of the Fibonacci numbers defined by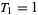 
, 
, 
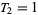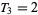, and the recurrence equation
 |
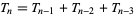(1) |
for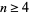 
(e.g., Develin 2000). They represent the 
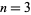case of the Fibonacci n-step numbers.
The first few terms using the above indexing convention for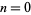 
, 1, 2, ... are 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... (OEIS A000073; which however adopts the alternate indexing convention 
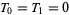and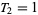 
).
The first few prime tribonacci numbers are 2, 7, 13, 149, 19341322569415713958901, ... (OEIS A092836), which have indices 3, 5, 6, 10, 86, 97, 214, 801, 4201, 18698, 96878, ... (OEIS A092835), and no others with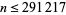 
(E. W. Weisstein, Mar. 21, 2009).
Using Brown's criterion, it can be shown that the tribonacci numbers are complete; that is, every positive number can be written as the sum of distinct tribonacci numbers. Moreover, every positive number has a unique Zeckendorf-like expansion as the sum of distinct tribonacci numbers and that sum does not contain three consecutive tribonacci numbers. The Zeckendorf-like expansion can be computed using a greedy algorithm.
An exact expression for the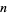 
th tribonacci number can be given explicitly by
 |
 |
 |
(2) |
 |
 |
 |
(3) |
where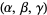 
are the three roots of the polynomial
 |
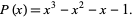(4) |
This can be written in slightly more concise form as
 |
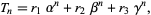(5) |
where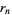 
is the 
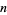th root of the polynomial
 |
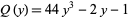(6) |
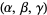and 
and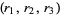 
are in the ordering of the Wolfram Language's Root object.
The tribonacci numbers can also be computed using the generating function
 |
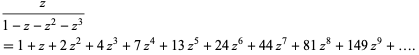(7) |
Another explicit formula for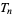 
is also given by
|
(8) |
where ![[x]](https://mathworld.wolfram.com/images/equations/TribonacciNumber/Inline23.gif)
denotes the nearest integer function (Plouffe). The first part of the numerator is related to the real root of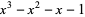 
, but determination of the denominator requires an application of the LLL algorithm.
The ratio of adjacent terms tends to the positive real root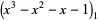 
, namely 1.83929... (OEIS A058265), sometimes known as the tribonacci constant.
By considering the series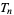 
(mod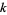 
), one can prove that any integer 
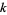is a factor of 
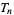for some 
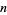(Brenner 1954). The smallest values of 
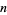for which 
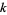is a factor for 
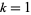, 2, ... are given by 1, 3, 7, 4, 14, 7, 5, 7, 9, 19, 8, 7, 6, ... (OEIS A112305).
The tribonacci constant is extremely prominent in the properties of the snub cube, its dual the pentagonal icositetrahedron, and the snub cube-pentagonal icositetrahedron compound. It can even be used to express the hard hexagon entropy constant.
With different initial values, the tribonacci sequence starts as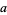 
, 
, 
, 
, 
, 
, 
, 
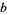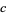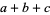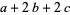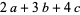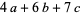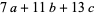, ..., which gives the following sequences as special cases.
 |
 |
 |
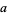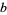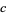OEIS | sequence |
| 0 | 0 | 1 | A000073 | 0, 1, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, ... |
| 1 | 1 | 1 | A000213 | 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, ... |
| 0 | 1 | 0 | A001590 | 0, 1, 0, 1, 2, 3, 6, 11, 20, 37, 68, 125, 230, ... |
| 3 | 1 | 3 | A001644 | 3, 1, 3, 7, 11, 21, 39, 71, 131, 241, 443, 815, ... |
 |
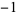2 | 2 | A100683 | 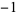 , 2, 2, 3, 7, 12, 22, 41, 75, 138, 254, 467, ... |
REFERENCES:
Brenner, J. L. "Linear Recurrence Relations." Amer. Math. Monthly 61, 171-173, 1954.
Develin, M. "A Complete Categorization of When Generalized Tribonacci Sequences Can Be Avoided by Additive Partitions." Electronic J. Combinatorics 7, No. 1, R53, 1-7, 2000. https://www.combinatorics.org/Volume_7/Abstracts/v7i1r53.html.
Dumitriu, I. "On Generalized Tribonacci Sequences and Additive Partitions." Disc. Math. 219, 65-83, 2000.
Feinberg, M. "Fibonacci-Tribonacci." Fib. Quart. 1, 71-74, 1963.
Hoggatt, V. E. Jr. "Additive Partitions of the Positive Integers." Fib. Quart. 18, 220-226, 1980.
Plouffe, S. "The Tribonacci Constant." https://pi.lacim.uqam.ca/piDATA/tribo.txt.
Sloane, N. J. A. Sequences A000073/M1074, A000213/M2454, A001590/M0784, A001644/M2625, A058265, A092835, A092836, A100683,and A112305 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
