Repunit
A repunit is a number consisting of copies of the single digit 1. The term "repunit" was coined by Beiler (1966), who also gave the first tabulation of known factors.
In base-10, repunits have the form
Repunits  therefore have exactly
therefore have exactly  decimal digits. Amazingly, the squares of the repunits
decimal digits. Amazingly, the squares of the repunits  give the Demlo numbers,
give the Demlo numbers,  ,
,  ,
,  , ... (OEIS A002275 and A002477).
, ... (OEIS A002275 and A002477).
The number of factors for the base-10 repunits for 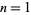 , 2, ... are 1, 1, 2, 2, 2, 5, 2, 4, 4, 4, 2, 7, 3, ... (OEIS A046053). The base-10 repunit probable primes
, 2, ... are 1, 1, 2, 2, 2, 5, 2, 4, 4, 4, 2, 7, 3, ... (OEIS A046053). The base-10 repunit probable primes 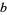 occur for
occur for 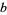 , 19, 23, 317, and 1031, 49081, 86453, 109297, and 270343 (OEIS A004023; Madachy 1979, Williams and Dubner 1986, Ball and Coxeter 1987, Granlund, Dubner 1999, Baxter 2000), where
, 19, 23, 317, and 1031, 49081, 86453, 109297, and 270343 (OEIS A004023; Madachy 1979, Williams and Dubner 1986, Ball and Coxeter 1987, Granlund, Dubner 1999, Baxter 2000), where 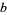 is the largest proven prime (Williams and Dubner 1986). T. Granlund completed a search up to
is the largest proven prime (Williams and Dubner 1986). T. Granlund completed a search up to 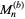 in 1998 using two months of CPU time on a parallel computer. The search was extended by Dubner (1999), culminating in the discovery of the probable prime
in 1998 using two months of CPU time on a parallel computer. The search was extended by Dubner (1999), culminating in the discovery of the probable prime 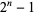 . A number of larger repunit probable primes have since been found, as summarized in the following table.
. A number of larger repunit probable primes have since been found, as summarized in the following table.
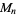 |
discoverer(s) |
date |
| 49081 |
H. Dubner (1999, 2002) |
Sep. 9, 1999 |
| 86453 |
L. Baxter (2000) |
Oct. 26, 2000 |
| 109297 |
P. Bourdelais (2007), H. Dubner (2007) |
Mar. 26-28, 2007 |
| 270343 |
M. Voznyy and A. Budnyy (2007) |
Jul. 11, 2007 |
Every prime repunit is a circular prime.
Repunit can be generalized to base 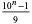 , giving a base-
, giving a base-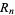 repunit as number of the form
repunit as number of the form
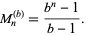 |
(3)
|
This gives the special cases summarized in the following table.
 |
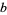 |
name |
| 2 |
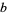 |
Mersenne number 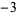 |
| 10 |
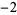 |
repunit 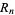 |
The idea of repunits can also be extended to negative bases. Except for requiring 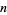 to be odd, the math is very similar (Dubner and Granlund 2000).
to be odd, the math is very similar (Dubner and Granlund 2000).
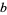 |
OEIS |
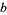 -repunits -repunits |
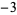 |
A066443 |
1, 7, 61, 547, 4921, 44287, 398581, ... |
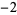 |
A007583 |
1, 3, 11, 43, 171, 683, 2731, ... |
| 2 |
A000225 |
1, 3, 7, 15, 31, 63, 127, ... |
| 3 |
A003462 |
1, 4, 13, 40, 121, 364, ... |
| 4 |
A002450 |
1, 5, 21, 85, 341, 1365, ... |
| 5 |
A003463 |
1, 6, 31, 156, 781, 3906, ... |
| 6 |
A003464 |
1, 7, 43, 259, 1555, 9331, ... |
| 7 |
A023000 |
1, 8, 57, 400, 2801, 19608, ... |
| 8 |
A023001 |
1, 9, 73, 585, 4681, 37449, ... |
| 9 |
A002452 |
1, 10, 91, 820, 7381, 66430, ... |
| 10 |
A002275 |
1, 11, 111, 1111, 11111, ... |
| 11 |
A016123 |
1, 12, 133, 1464, 16105, 177156, ... |
| 12 |
A016125 |
1, 13, 157, 1885, 22621, 271453, ... |
Williams and Seah (1979) factored generalized repunits for 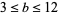 and
and 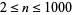 . A (base-10) repunit can be prime only if
. A (base-10) repunit can be prime only if 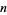 is prime, since otherwise
is prime, since otherwise 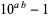 is a binomial number which can be factored algebraically. In fact, if
is a binomial number which can be factored algebraically. In fact, if 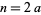 is even, then
is even, then 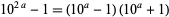 . As with positive bases, all the exponents of prime repunits with negative bases are also prime.
. As with positive bases, all the exponents of prime repunits with negative bases are also prime.
 |
OEIS |
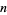 of prime of prime 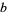 -repunits -repunits |
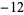 |
A057178 |
5, 11, 109, 193, 1483, ... |
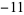 |
A057177 |
5, 7, 179, 229, 439, 557, 6113, ... |
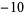 |
A001562 |
5, 7, 19, 31, 53, 67, 293, ... |
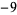 |
A057175 |
3, 59, 223, 547, 773, 1009, 1823, ... |
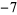 |
A057173 |
3, 17, 23, 29, 47, 61, 1619, ... |
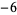 |
A057172 |
3, 11, 31, 43, 47, 59, 107, ... |
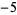 |
A057171 |
5, 67, 101, 103, 229, 347, 4013, ... |
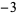 |
A007658 |
3, 5, 7, 13, 23, 43, 281, ... |
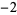 |
A000978 |
3, 5, 7, 11, 13, 17, 19, ... |
| 2 |
A000043 |
2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, ... |
| 3 |
A028491 |
3, 7, 13, 71, 103, 541, 1091, 1367, ... |
| 5 |
A004061 |
3, 7, 11, 13, 47, 127, 149, 181, 619, ... |
| 6 |
A004062 |
2, 3, 7, 29, 71, 127, 271, 509, 1049, ... |
| 7 |
A004063 |
5, 13, 131, 149, 1699, ... |
| 10 |
A004023 |
2, 19, 23, 317, 1031, ... |
| 11 |
A005808 |
17, 19, 73, 139, 907, 1907, 2029, 4801, ... |
| 12 |
A004064 |
2, 3, 5, 19, 97, 109, 317, 353, 701, ... |
Yates (1982) published all the repunit factors for 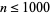 , a portion of which are reproduced in the Wolfram Language notebook by Weisstein. Brillhart et al. (1988) gave a table of repunit factors which cannot be obtained algebraically, and a continuously updated version of this table is now maintained online. These tables include factors for
, a portion of which are reproduced in the Wolfram Language notebook by Weisstein. Brillhart et al. (1988) gave a table of repunit factors which cannot be obtained algebraically, and a continuously updated version of this table is now maintained online. These tables include factors for 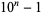 (with
(with 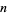 odd) and
odd) and 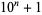 (with
(with 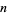 even and odd). After algebraically factoring
even and odd). After algebraically factoring 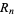 , these types of factors are sufficient for complete factorizations.
, these types of factors are sufficient for complete factorizations.
The sequence of least 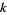 such that
such that 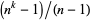 is prime for
is prime for 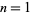 , 2, ... are 2, 3, 2, 3, 2, 5, 3, 0, 2, 17, 2, 5, ... (OEIS A084740), and the sequence of least
, 2, ... are 2, 3, 2, 3, 2, 5, 3, 0, 2, 17, 2, 5, ... (OEIS A084740), and the sequence of least 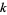 such that
such that 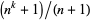 is prime for
is prime for 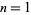 , 2, ... are 3, 3, 3, 5, 3, 3, 0, 3, 5, 5, 5, 3, ... (OEIS A084742).
, 2, ... are 3, 3, 3, 5, 3, 3, 0, 3, 5, 5, 5, 3, ... (OEIS A084742).
A Smith number can be constructed from every factored repunit.
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 66, 1987.
Baxter, L. "R86453 Is a New Probable Prime Repunit." 26 Oct 2000. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0010&L=nmbrthry&P=2557.
Beiler, A. H. "11111...111." Ch. 11 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Brillhart, J.; Lehmer, D. H.; Selfridge, J.; Wagstaff, S. S. Jr.; and Tuckerman, B. Factorizations of b-n+/-1, b=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers, rev. ed. Providence, RI: Amer. Math. Soc., 1988.
Di Maria, G. "The Repunit Primes Project." https://www.repunit.org/.
Dubner, H. "Generalized Repunit Primes." Math. Comput. 61, 927-930, 1993.
Dubner, H. "New prp Repunit R(49081)." 9 Sep 1999. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9909&L=nmbrthry&P=740.
Dubner, H. "Repunit 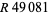 is a Probable Prime." Math. Comput. 71, 833-835, 2002. https://www.ams.org/mcom/2002-71-238/.
is a Probable Prime." Math. Comput. 71, 833-835, 2002. https://www.ams.org/mcom/2002-71-238/.
Dubner, H. "New Repunit R(109297)." 3 Apr 2007. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0704&L=nmbrthry&T=0&P=178.
Dubner, H. and Granlund, T. "Primes of the Form 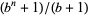 ." J. Int. Sequences 3, No. 00.2.7, 2000. https://www.cs.uwaterloo.ca/journals/JIS/VOL3/DUBNER/dubner.html.
." J. Int. Sequences 3, No. 00.2.7, 2000. https://www.cs.uwaterloo.ca/journals/JIS/VOL3/DUBNER/dubner.html.
Dudeney, H. E. The Canterbury Puzzles and Other Curious Problems, 7th ed. London: Thomas Nelson and Sons, 1949.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 85-86, 1984.
Granlund, T. "Repunits." https://www.swox.com/gmp/repunit.html.
Guy, R. K. "Mersenne Primes. Repunits. Fermat Numbers. Primes of Shape 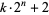 ." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.
." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 152-153, 1979.
Ribenboim, P. "Repunits and Similar Numbers." §5.5 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 350-354, 1996.
Sloane, N. J. A. Sequences A000043/M0672, A000225/M2655, A000978, A001562, A002275, A002477/M5386, A002450/M3914, A002452/M4733, A003462/M3463, A007583, A007658, A003463/M4209, A003464/M4425, A004023/M2114, A004023/M2114, A004061/M2620, A004062/M0861, A004063/M3836, A004064/M0744, A005808/M5032, A016123, A016125, A023000, A023001, A028491/M2643, A046053, A057171, A057172, A057173, A057175, A057177, A057178, A066443, A084740, and A084742 in "The On-Line Encyclopedia of Integer Sequences."
Snyder, W. M. "Factoring Repunits." Am. Math. Monthly 89, 462-466, 1982.
Sorli, R. "Factorization Tables." https://www-staff.maths.uts.edu.au/~rons/fact/fact.htm.
Voznyy, M. and Budnyy, A. "New PRP Repunit R(270343)." 15 Jul 2007. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0707&L=nmbrthry&T=0&P=1086.
Williams, H. C. and Dubner, H. "The Primality of 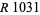 ." Math. Comput. 47, 703-711, 1986.
." Math. Comput. 47, 703-711, 1986.
Williams, H. C. and Seah, E. "Some Primes of the Form 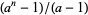 . Math. Comput. 33, 1337-1342, 1979.
. Math. Comput. 33, 1337-1342, 1979.
Yates, S. "Peculiar Properties of Repunits." J. Recr. Math. 2, 139-146, 1969.
Yates, S. "Prime Divisors of Repunits." J. Recr. Math. 8, 33-38, 1975.
Yates, S. "The Mystique of Repunits." Math. Mag. 51, 22-28, 1978.
Yates, S. Repunits and Reptends. Delray Beach, FL: S. Yates, 1982.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


