
Pollard rho Factorization Method
 المؤلف:
Brent, R.
المؤلف:
Brent, R.
 المصدر:
"An Improved Monte Carlo Factorization Algorithm." Nordisk Tidskrift for Informationsbehandlung (BIT) 20
المصدر:
"An Improved Monte Carlo Factorization Algorithm." Nordisk Tidskrift for Informationsbehandlung (BIT) 20
 الجزء والصفحة:
...
الجزء والصفحة:
...
 14-9-2020
14-9-2020
 1818
1818
Pollard rho Factorization Method
A prime factorization algorithm also known as Pollard Monte Carlo factorization method. There are two aspects to the Pollard 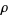 factorization method. The first is the idea of iterating a formula until it falls into a cycle. Let
factorization method. The first is the idea of iterating a formula until it falls into a cycle. Let 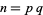 , where
, where 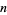 is the number to be factored and
is the number to be factored and 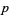 and
and 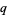 are its unknown prime factors. Iterating the formula
are its unknown prime factors. Iterating the formula
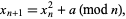 |
(1)
|
or almost any polynomial formula (an exception being 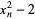 ) for any initial value
) for any initial value 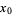 will produce a sequence of number that eventually fall into a cycle. The expected time until the
will produce a sequence of number that eventually fall into a cycle. The expected time until the 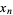 s become cyclic and the expected length of the cycle are both proportional to
s become cyclic and the expected length of the cycle are both proportional to 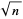 .
.
However, since 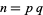 with
with 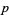 and
and 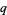 relatively prime, the Chinese remainder theorem guarantees that each value of
relatively prime, the Chinese remainder theorem guarantees that each value of  (mod
(mod 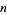 ) corresponds uniquely to the pair of values (
) corresponds uniquely to the pair of values (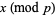 ),
), 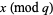 ). Furthermore, the sequence of
). Furthermore, the sequence of 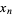 s follows exactly the same formula modulo
s follows exactly the same formula modulo 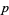 and
and 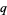 , i.e.,
, i.e.,
Therefore, the sequence (mod 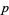 ) will fall into a much shorter cycle of length on the order of
) will fall into a much shorter cycle of length on the order of 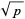 . It can be directly verified that two values
. It can be directly verified that two values 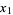 and
and 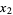 have the same value (mod
have the same value (mod 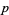 ), by computing
), by computing
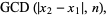 |
(4)
|
which is equal to 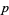 .
.
The second part of Pollard's method concerns detection of the fact that a sequence has become periodic. Pollard's suggestion was to use the idea attributed to Floyd of comparing 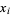 to
to 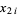 for all
for all 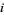 . A different method is used in Brent's factorization method.
. A different method is used in Brent's factorization method.
Under worst conditions, the Pollard 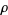 algorithm can be very slow.
algorithm can be very slow.
REFERENCES:
Brent, R. "An Improved Monte Carlo Factorization Algorithm." Nordisk Tidskrift for Informationsbehandlung (BIT) 20, 176-184, 1980.
Brent, R. P. "Some Integer Factorization Algorithms Using Elliptic Curves." Austral. Comp. Sci. Comm. 8, 149-163, 1986.
Bressoud, D. M. Factorization and Primality Testing. New York: Springer-Verlag, pp. 61-67, 1989.
Eldershaw, C. and Brent, R. P. "Factorization of Large Integers on Some Vector and Parallel Computers."
Montgomery, P. L. "Speeding the Pollard and Elliptic Curve Methods of Factorization." Math. Comput. 48, 243-264, 1987.
Pollard, J. M. "A Monte Carlo Method for Factorization." Nordisk Tidskrift for Informationsbehandlung (BIT) 15, 331-334, 1975.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 83 and 102-103, 1991.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


