
Hardy-Littlewood Conjectures
 المؤلف:
Hardy, G. H. and Littlewood, J. E.
المؤلف:
Hardy, G. H. and Littlewood, J. E.
 المصدر:
"Some Problems of Partitio Numerorum. III. On the Expression of a Number as a Sum of Primes." Acta Math. 44
المصدر:
"Some Problems of Partitio Numerorum. III. On the Expression of a Number as a Sum of Primes." Acta Math. 44
 الجزء والصفحة:
...
الجزء والصفحة:
...
 6-9-2020
6-9-2020
 2617
2617
Hardy-Littlewood Conjectures
The first Hardy-Littlewood conjecture is called the k-tuple conjecture. It states that the asymptotic number of prime constellations can be computed explicitly. A particular case gives the so-called strong twin prime conjecture
The second Hardy-Littlewood conjecture states that
for all 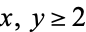 , where
, where 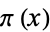 is the prime counting function.
is the prime counting function.
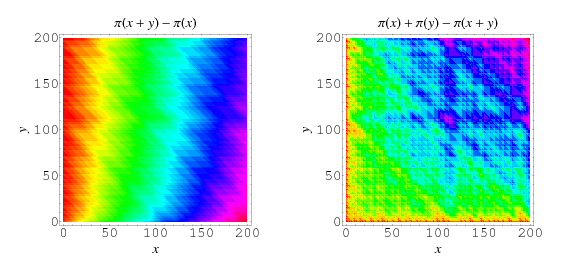
The following table summarizes the first few values of 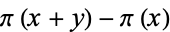 for integer
for integer 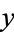 and
and 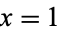 , 2, .... The values of this function are plotted above.
, 2, .... The values of this function are plotted above.
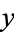 |
OEIS |
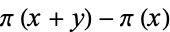 for for 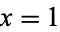 , 2, ... , 2, ... |
| 1 |
A080545 |
1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, ... |
| 2 |
A090405 |
2, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, ... |
| 3 |
A090406 |
2, 2, 1, 2, 1, 1, 0, 1, 1, 2, 1, 1, 0, 1, 1, 2, 1, 1, 0, ... |
Although it is not obvious, Richards (1974) proved that the first and second conjectures are incompatible with each other.
REFERENCES:
Guy, R. K. §A9 in Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, 2004.
Hardy, G. H. and Littlewood, J. E. "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes." Acta Math. 44, 1-70, 1923.
Richards, I. "On the Incompatibility of Two Conjectures Concerning Primes." Bull. Amer. Math. Soc. 80, 419-438, 1974.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 61-62 and 68-69, 1994.
Sloane, N. J. A. Sequences A080545, A090405, A090406, in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


