المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر
أضيف حديثاً
تنفيذ وتقييم خطة إعادة الهيكلة (إعداد خطة إعادة الهيكلة1)
2024-11-05
مـعاييـر تحـسيـن الإنـتاجـيـة
2024-11-05
نـسـب الإنـتاجـيـة والغـرض مـنها
2024-11-05
المـقيـاس الكـلـي للإنتاجـيـة
2024-11-05
الإدارة بـمؤشـرات الإنـتاجـيـة (مـبادئ الإنـتـاجـيـة)
2024-11-05
زكاة الفطرة
2024-11-05

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
pluralia tantum
2023-10-28
التذكير بأحقية امير المؤمنين بالخلافة
25-01-2015
التحسس عن طريق الانجذاب للطاقة
15-1-2016
آثار الإخلاص
2024-08-08
سقوط حرف الجر من الفعل المتعدي بواسطة
17-10-2014
طريق تحصيل الشكر.
2024-03-17

Bombieri,s Theorem  
  
964   04:21 مساءً   date: 16-8-2020
Author : Bombieri, E.
Book or Source : "On the Large Sieve." Mathematika 12
Page and Part : ...


Read More
Super-d Number
Date: 19-11-2020 895
Diophantine Equation--2nd Powers
Date: 20-5-2020 1784
Brocard,s Conjecture
Date: 25-8-2020 777

Bombieri's Theorem

Define

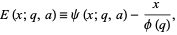E(x;q,a)=psi(x;q,a)-x/(phi(q)),

(1)

where

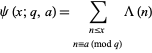psi(x;q,a)=sum_(n<=x; n=a (mod q))Lambda(n)

(2)

(Davenport 1980, p. 121), 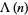Lambda(n) is the Mangoldt function, and 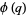phi(q) is the totient function. Now define

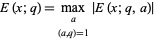E(x;q)=max_(a; (a,q)=1)|E(x;q,a)|

(3)

where the sum is over 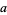a relatively prime to 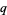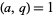q, (a,q)=1, and

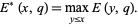E^*(x,q)=max_(y<=x)E(y,q).

(4)

Bombieri's theorem then says that for fixed 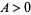A>0,

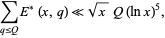sum_(q<=Q)E^*(x,q)<<sqrt(x)Q(lnx)^5,

(5)

provided that 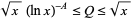sqrt(x)(lnx)^(-A)<=Q<=sqrt(x).

REFERENCES:

Bombieri, E. "On the Large Sieve." Mathematika 12, 201-225, 1965.

Davenport, H. "Bombieri's Theorem." Ch. 28 in Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, pp. 161-168, 1980.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
التاريخ / 2024-11-04

الأخبار العلمية
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
التاريخ / 2024-11-04

الساحة الاسلامية
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
التاريخ / 2024-11-05