Strong Law of Large Numbers
المؤلف:
Feller, W.
المصدر:
"The Strong Law of Large Numbers." §10.7 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley
الجزء والصفحة:
...
7-8-2020
936
Strong Law of Large Numbers
The sequence of variates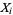 
with corresponding means 
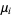obeys the strong law of large numbers if, to every pair 
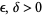, there corresponds an 
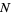such that there is probability 
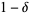or better that for every 
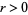, all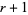 
inequalities
 |
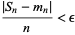(1)
|
for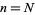 
, 
, ..., 
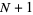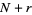will be satisfied, where
(Feller 1968). Kolmogorov established that the convergence of the sequence
 |
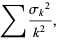(4)
|
sometimes called the Kolmogorov criterion, is a sufficient condition for the strong law of large numbers to apply to the sequence of mutually independent random variables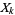 
with variances 
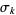(Feller 1968).
REFERENCES:
Feller, W. "The Strong Law of Large Numbers." §10.7 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 243-245, 1968.
Feller, W. "Strong Laws for Martingales." §7.8 in An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, pp. 234-238, 1971.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
