
j-Invariant
 المؤلف:
Berwick, W. E. H.
المؤلف:
Berwick, W. E. H.
 المصدر:
"Modular Invariants Expressible in Terms of Quadratic and Cubic Irrationalities." Proc. London Math. Soc. 28
المصدر:
"Modular Invariants Expressible in Terms of Quadratic and Cubic Irrationalities." Proc. London Math. Soc. 28
 الجزء والصفحة:
...
الجزء والصفحة:
...
 8-7-2020
8-7-2020
 2372
2372
j-Invariant
An invariant of an elliptic curve given in the form
which is closely related to the elliptic discriminant and defined by
The determination of 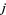 as an algebraic integer in the quadratic field
as an algebraic integer in the quadratic field 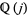 is discussed by Greenhill (1891), Weber (1902), Berwick (1928), Watson (1938), Gross and Zaiger (1985), and Dorman (1988). The norm of
is discussed by Greenhill (1891), Weber (1902), Berwick (1928), Watson (1938), Gross and Zaiger (1985), and Dorman (1988). The norm of 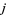 in
in 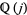 is the cube of an integer in
is the cube of an integer in 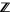 .
.
REFERENCES:
Berwick, W. E. H. "Modular Invariants Expressible in Terms of Quadratic and Cubic Irrationalities." Proc. London Math. Soc. 28, 53-69, 1928.
Dorman, D. R. "Special Values of the Elliptic Modular Function and Factorization Formulae." J. reine angew. Math. 383, 207-220, 1988.
Greenhill, A. G. "Table of Complex Multiplication Moduli." Proc. London Math. Soc. 21, 403-422, 1891.
Gross, B. H. and Zaiger, D. B. "On Singular Moduli." J. reine angew. Math. 355, 191-220, 1985.
Stepanov, S. A. "The 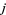 -Invariant." §7.2 in Codes on Algebraic Curves. New York: Kluwer, pp. 178-180, 1999.
-Invariant." §7.2 in Codes on Algebraic Curves. New York: Kluwer, pp. 178-180, 1999.
Watson, G. N. "Ramanujans Vermutung über Zerfällungsanzahlen." J. reine angew. Math. 179, 97-128, 1938.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1979.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


