The conjecture that there are only finitely many triples of relatively prime integer powers 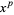, , 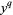 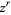for which

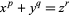(1)

with

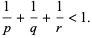(2)

Darmon and Merel (1997) have shown that there are no relatively prime solutions 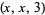 with 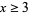. Ten solutions are known,

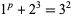(3)

for 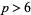, and

			(4)
			(5)
			(6)
			(7)
			(8)
			(9)
			(10)
			(11)
			(12)

(Mauldin 1997).

The following table summarizes known solutions (Poonen et al. 2005). Any remaining solutions would satisfy the Tijdeman-Zagier conjecture, also known popularly as Beal's conjecture (Elkies 2007).

exponents	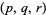reference
(2, 3, 7)	Poonen et al. (2005)
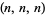	Wiles
(2, 3, 8), (2, 3, 9), (2, 4, 5),	Bruin (2004)
(2, 4, 6), (3, 3, 4), (3, 3, 5)
(2, 4, 7)	Ghioca
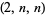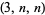,	Darmon-Merel
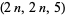	Bennett
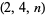	Bennett-Skinner

It is not known if the analogous conjecture for , , 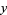and 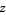 Gaussian integers holds. Known solutions include

			(13)
			(14)

(E. Pegg Jr., pers. comm., March 30, 2002).

REFERENCES:

Bruin, N. "Visualising Sha[2] in Abelian Surfaces." Math. Comput. 73, 1459--1476, 2004.

Darmon, H. and Granville, A. "On the Equations 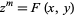 and 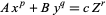." Bull. London Math. Soc. 27, 513-543, 1995.

Darmon, H. and Merel, L. "Winding Quotients and Some Variants of Fermat's Last Theorem." J. reine angew. Math. 490, 81-100, 1997.

Elkies, N. "The ABCs of Number Theory." Harvard Math. Rev. 1, 64-76, 2007.

Mauldin, R. D. "A Generalization of Fermat's Last Theorem: The Beal Conjecture and Prize Problem." Not. Amer. Math. Soc. 44, 1436-1437, 1997.

Poonen, B.; Schaefer, E. F.; and Stoll, M. "Twists of 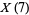 and Primitive Solutions to 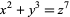." 10 Aug 2005. https://arxiv.org/abs/math/0508174.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يقيم مسابقة الكوثر الخاصة بترتيل القرآن الكريم في كربلاء

قسم الشؤون الفكرية والثقافية يُصدر العدد الثالث والعشرين من مجلّة (أوراق معرفية)

قسم التربية والتعليم يُطلق الموسم التدريبيّ الصيفيّ لملاكات مجموعة العميد التربوية

المجمَع العلمي يُطلق المرحلة الثالثة من مشروع أمير القرّاء الوطني

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد