As a part of the study of Waring's problem, it is known that every positive integer is a sum of no more than 9 positive cubes (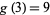), that every "sufficiently large" integer is a sum of no more than 7 positive cubes (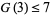; although it is not known if 7 can be reduced), and that every integer is a sum of at most 5 signed cubes (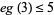; although it is not known if 5 can be reduced to 4).

It is known that every 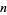 can be written in the form

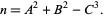(1)

An elliptic curve of the form 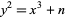 for 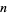 an integer is known as a Mordell curve.

The 3.1.2 equation

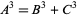(2)

is a case of Fermat's last theorem with 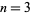. In fact, this particular case was known not to have any solutions long before the general validity of Fermat's last theorem was established. Thue showed that a Diophantine equation of the form

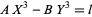(3)

for 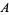, , 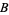and 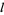 integers, has only finite many solutions (Hardy 1999, pp. 78-79).

Miller and Woollett (1955) and Gardiner et al. (1964) investigated integer solutions of

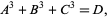(4)

i.e., numbers representable as the sum of three (positive or negative) cubic numbers.

The general rational solution to the 3.1.3 equation

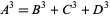(5)

was found by Euler and Vieta (Hardy 1999, pp. 20-21; Dickson 2005, pp. 550-554). Hardy and Wright (1979, pp. 199-201) give a solution which can be based on the identities

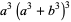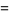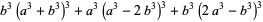			(6)
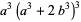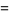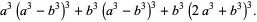			(7)

This is equivalent to the general 3.2.2 solution found by Ramanujan (Berndt 1994, pp. 54 and 107; Hardy 1999, p. 11, 68, and 237; Dickson 2005, pp. 500 and 554). A partial quadratic form identity was also given by Ramanujan (Berndt 1994, p. 56)

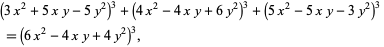(8)

the first instance of which gives the nice equation , which is one of Plato's numbers. Such partial quadratic form parametrizations can be found using the identity

(9)

where , , and , and is reduced to finding solutions to  (or the sum may be any number of cubes), which is just a special case of an even more general identity (Piezas 2005).

The 22 smallest integer solutions are

			(10)
			(11)
			(12)
			(13)
			(14)
			(15)
			(16)
			(17)
			(18)
			(19)
			(20)
			(21)
			(22)
			(23)
			(24)
			(25)
			(26)
			(27)
			(28)
			(29)
			(30)
			(31)

Other small solutions include

			(32)
			(33)
			(34)
			(35)
			(36)
			(37)
			(38)
			(39)
			(40)
			(41)
			(42)
			(43)
			(44)
			(45)
			(46)
			(47)
			(48)
			(49)

(Fredkin 1972; Madachy 1979, pp. 124 and 141; Dutch). A database with sum  for all  is maintained by Wroblewski.

Other general solutions have been found by Binet (1841) and Schwering (1902), although Ramanujan's formulation is the simplest. No general solution giving all positive integral solutions is known (Dickson 2005, pp. 550-561). Y. Kohmoto has found a  solution,

			(50)
			(51)
			(52)
			(53)
			(54)
			(55)
			(56)
			(57)
			(58)

3.1.4 equations include

			(59)
			(60)

3.1.5 equations include

			(61)
			(62)

and a 3.1.6 equation is given by

(63)

The 3.2.2 equation

(64)

has a known parametric solution (Guy 1994, p. 140; Dickson 2005, pp. 550-554), and 10 solutions with sum ,

			(65)
			(66)
			(67)
			(68)
			(69)
			(70)
			(71)
			(72)
			(73)
			(74)

(OEIS A001235; Moreau 1898). The first number (Madachy 1979, pp. 124 and 141) in this sequence, the so-called Hardy-Ramanujan number, is associated with a story told about Ramanujan by G. H. Hardy, but was known as early as 1657 (Berndt and Bhargava 1993). The smallest number representable in  ways as a sum of cubes is called the th taxicab number.

Ramanujan gave a general solution to the 3.2.2 equation as

(75)

where

(76)

(Berndt and Bhargava 1993; Berndt 1994, p. 107). Another form due to Ramanujan is

(77)

Hardy and Wright (1979, Theorem 412) prove that there are numbers that are expressible as the sum of two cubes in  ways for any  (Guy 1994, pp. 140-141). The proof is constructive, providing a method for computing such numbers: given rationals numbers  and , compute

			(78)
			(79)
			(80)
			(81)

Then

(82)

The denominators can now be cleared to produce an integer solution. If  is picked to be large enough, the  and  will be positive. If  is still larger, the  will be large enough for  and  to be used as the inputs to produce a third pair, etc. However, the resulting integers may be quite large, even for . E.g., starting with , the algorithm finds

(83)

giving

			(84)
			(85)

The numbers representable in three ways as a sum of two cubes (a  equation) are

			(86)
			(87)
			(88)
			(89)
			(90)

(Guy 1994, OEIS A003825). Wilson (1997) found 32 numbers representable in four ways as the sum of two cubes (a  equation). The first is

(91)

The smallest known numbers so representable are 6963472309248, 12625136269928, 21131226514944, 26059452841000, ... (OEIS A003826). Wilson also found six five-way sums,

	(92)
	(93)
	(94)
	(95)
	(96)
	(97)
	(98)
	(99)
	(100)
	(101)
	(102)
	(103)
	(104)
	(105)
	(106)
	(107)
	(108)
	(109)
	(110)
	(111)
	(112)
	(113)
	(114)
	(115)
	(116)
	(117)
	(118)
	(119)
	(120)
	(121)

and a single six-way sum

(122)

A solution to the 3.4.4 equation is

(123)

(Madachy 1979, pp. 118 and 133).

3.6.6 equations also exist:

	(124)
	(125)
	(126)

(Madachy 1979, p. 142; Chen Shuwen).

In 1756-1757, Euler (1761, 1849, 1915) gave a parametric solution to

(127)

as

			(128)
			(129)
			(130)

although relatively prime solutions require the use of fractional values of  (Dickson 2005, p. 578). To avoid this, Euler also gave the solutions

			(131)
			(132)
			(133)

for , and

			(134)
			(135)
			(136)

for  (Dickson 2005, p. 579).

REFERENCES:

Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.

Berndt, B. C. and Bhargava, S. "Ramanujan--For Lowbrows." Amer. Math. Monthly 100, 645-656, 1993.

Binet, J. P. M. "Note sur une question relative à la théorie des nombres." C. R. Acad. Sci. (Paris) 12, 248-250, 1841.

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.

Dutch, S. "Cubic Quartets with 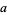, , 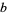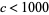." https://www.uwgb.edu/dutchs/RECMATH/Cubesums.htm.

Euler, L. Novi. Comm. Acad. Petrop. 6 (ad annos 1756-1757), p. 181, 1761.

Euler, L. Comm. Arith. Coll. 1, 207, 1849.

Euler, L. Opera Omnia, Series Prima, Vol. 2. Leipzig, Germany: Teubner, p. 454, 1915.

Fredkin, E. Item 58 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 23, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item58.

Gardiner, V. L.; Lazarus, R. B.; and Stein, P. R. "Solutions of the Diophantine Equation 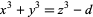." Math. Comput. 18, 408-413, 1964.

Guy, R. K. "Sums of Like Powers. Euler's Conjecture." §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Koyama, K.; Tsuruoka, Y.; and Sekigawa, H. "On Searching for Solutions of the Diophantine Equation 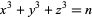." Math. Comput. 66, 841-851, 1997.

Kraus, A. "Sur l'équation 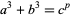." Experim. Math. 7, 1-13, 1998.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, 1979.

Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.

Miller, J. C. P. and Woollett, M. F. C. "Solutions of the Diophantine Equation 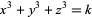." J. London Math. Soc. 30, 101-110, 1955.

Moreau, C. "Plus petit nombre égal à la somme de deux cubes de deux façons." L'Intermediaire Math. 5, 66, 1898.

Nagell, T. "The Diophantine Equation 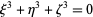 and Analogous Equations" and "Diophantine Equations of the Third Degree with an Infinity of Solutions." §65 and 66 in Introduction to Number Theory. New York: Wiley, pp. 241-248, 1951.

Piezas, T. "Ramanujan and the Cubic Equation 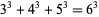." 2005. https://www.geocities.com/titus_piezas/RamCube.pdf.

Rivera, C. "Problems & Puzzles: Puzzle 048-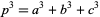,  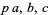Prime." https://www.primepuzzles.net/puzzles/puzz_048.htm.

Schwering, K. "Vereinfachte Lösungen des Eulerschen Aufgabe: 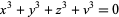." Arch. Math. Phys. 2, 280-284, 1902.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 157, 1993.

Sloane, N. J. A. Sequences A001235 and A003825 in "The On-Line Encyclopedia of Integer Sequences."

Wilson, D. Personal communication, Apr. 17, 1997.

Wroblewski, J. "Equal Sums of Powers--Tables." https://www.math.uni.wroc.pl/~jwr/eslp/tables.htm.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم التطوير يقيم دورة عن أخلاقيات المهنة للمنتسبين الجدد

تتضمن زيارة المراقد المقدسة في كربلاء.. معهد القرآن الكريم النسوي ينظم سفرة دينية لطالباته

المجمع العلمي يحتفي بذكرى ولادة الإمامين الباقر والهادي (عليهما السلام)

قسم الشؤون الفكرية يطلق فعاليات الأسبوع الثالث من برنامج البذرة الصالحة

المزيد

الآخبار الصحية

ثورة طبية.. الذكاء الاصطناعي يكشف سرطان الكلى في وقت قياسي

لتعزيز الطاقة والتغلب على التعب.. عليك بـ7 طرق بسيطة

لتحسين الهضم والتحكم في الشهية.. ما أفضل وقت لتناول التمر؟

خبراء يكشفون تأثير الاستحمام في الظلام على جودة النوم !

المزيد

الآخبار التكنلوجية

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

نظائر الهيليوم مقياس لاكتشاف رواسب الذهب.. كيف ذلك؟

الصين تطلق أول ناقلة نفط خام ذكية في العالم تعمل بالميثانول

الزمن على المريخ أسرع من الأرض.. دراسة علمية تكشف الفوارق

المزيد