The 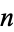-hypersphere (often simply called the 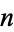-sphere) is a generalization of the circle (called by geometers the 2-sphere) and usual sphere (called by geometers the 3-sphere) to dimensions 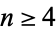. The 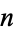-sphere is therefore defined (again, to a geometer; see below) as the set of 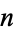-tuples of points (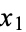, , 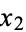..., 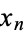) such that

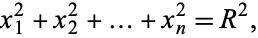(1)

where 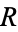 is the radius of the hypersphere.

Unfortunately, geometers and topologists adopt incompatible conventions for the meaning of "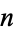-sphere," with geometers referring to the number of coordinates in the underlying space ("thus a two-dimensional sphere is a circle," Coxeter 1973, p. 125) and topologists referring to the dimension of the surface itself ("the 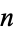-dimensional sphere  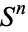is defined to be the set of all points  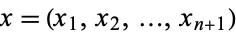in 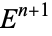 satisfying 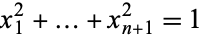," Hocking and Young 1988, p. 17; "the 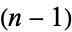-sphere  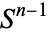is {x in R^n|d(x,0)=1}" src="https://mathworld.wolfram.com/images/equations/Hypersphere/Inline18.gif" style="height:18px; width:121px" />," Maunder 1997, p. 21). A geometer would therefore regard the object described by

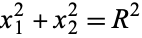(2)

as a 2-sphere, while a topologist would consider it a 1-sphere and denote it 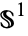. Similarly, a geometer would regard the object described by

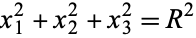(3)

as a 3-sphere, while a topologist would call it a 2-sphere and denote it . Extreme caution is therefore advised when consulting the literature. Following the literature, both conventions are used in this work, depending on context, which is stated explicitly wherever it might be ambiguous.

Let 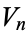 denote the content (i.e., 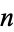-dimensional volume) of an 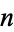-hypersphere (in the geometer's sense) of radius  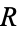is given by

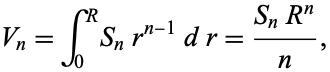(4)

where 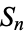 is the hyper-surface area of an 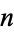-sphere of unit radius. A unit hypersphere must satisfy

			(5)
			(6)

But the gamma function can be defined by

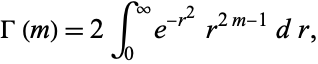(7)

so

(8)

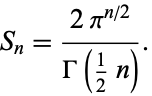(9)

Special forms of 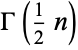 for 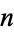 an integer allow the above expression to be written as

{(2^((n+1)/2)pi^((n-1)/2))/((n-2)!!) for n odd; (2pi^(n/2))/((1/2n-1)!) for n even, " src="https://mathworld.wolfram.com/images/equations/Hypersphere/NumberedEquation8.gif" style="height:98px; width:202px" />

(10)

where 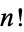 is a factorial and  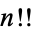is a double factorial (OEIS A072478 and A072479).

Strangely enough, for the unit hypersphere, the hyper-surface area reaches a maximum and then decreases towards 0 as 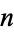 increases. The point of maximal hyper-surface area satisfies

(11)

where 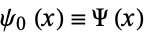 is the digamma function. This cannot be solved analytically for 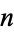, but the numerical solution is  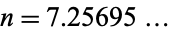(OEIS A074457; Wells 1986, p. 67). As a result, the seven-dimensional unit hypersphere has maximum hyper-surface area (Le Lionnais 1983; Wells 1986, p. 60).

In four dimensions, the generalization of spherical coordinates is given by

			(12)
			(13)
			(14)
			(15)

The equation for the 3-sphere 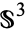 is therefore

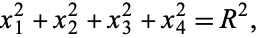(16)

and the line element is

(17)

By defining 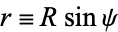, the line element can be rewritten

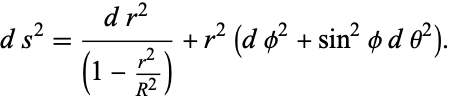(18)

The hyper-surface area is therefore given by

			(19)
			(20)

REFERENCES:

Collins, G. P. "The Shapes of Space." Sci. Amer. 291, 94-103, July 2004.

Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, p. 9, 1993.

Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973.

Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 58, 1983.

Maunder, C. M. C. Algebraic Topology. New York: Dover, 1997.

Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, pp. 96-101, 1988.

Sloane, N. J. A. Sequences A072478, A072479, and A074457 in "The On-Line Encyclopedia of Integer Sequences."

Sommerville, D. M. Y. An Introduction to the Geometry of n Dimensions. New York: Dover, p. 136, 1958.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الفكرية يطلق باقة من النشاطات الرقمية الخاصة بشهر المحرم

العتبة العباسية المقدسة تختتم السلسلة الأولى لمشروع المحاضرات القرآنية العاشورائية في بابل

العتبة العباسية المقدسة تسلّم راية العزاء إلى تجمّع مواكب محافظة الديوانية

قسم الشؤون الفكرية يواصل إقامة المجالس الحسينية ضمن سلسلة (بيوت النعيم)

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد