Twin Primes Constant
المؤلف:
Finch, S. R.
المصدر:
"Hardy-Littlewood Constants." §2.1 in Mathematical Constants. Cambridge, England: Cambridge University Press
الجزء والصفحة:
...
25-3-2020
2417
Twin Primes Constant
The twin primes constant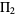 
(sometimes also denoted 
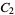) is defined by
where the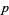 
s in sums and products are taken over primes only. This can be written as
![Pi_2=exp<span style=]() {(2-2^n)/n[P(n)-2^(-n)]}, " src="https://mathworld.wolfram.com/images/equations/TwinPrimesConstant/NumberedEquation1.gif" style="height:36px; width:190px" /> |
(5)
|
where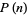 
is the prime zeta function.
Flajolet and Vardi (1996) give series with accelerated convergence
with
 |
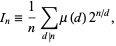(8)
|
where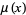 
is the Möbius function. The values of 
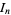for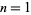 
, 2, ... are 2, 1, 2, 3, 6, 9, 18, 30, 56, 99, ... (OEIS A001037). Equation (7) has convergence like 
.
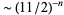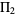was computed to 45 digits by Wrench (1961) and Gourdon and Sebah list 60 digits.
 |
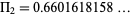(9)
|
(OEIS A005597). Le Lionnais (1983, p. 30) calls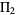 
the Shah-Wilson constant, and 
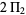the twin prime constant (Le Lionnais 1983, p. 37).
REFERENCES:
Finch, S. R. "Hardy-Littlewood Constants." §2.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 84-94, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Gourdon, X. and Sebah, P. "Some Constants from Number Theory." http://numbers.computation.free.fr/Constants/Miscellaneous/constantsNumTheory.html.
Hardy, G. H. and Littlewood, J. E. "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes." Acta Math. 44, 1-70, 1923.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 202, 1989.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, p. 147, 1991.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 61-66, 1994.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 30, 1993.
Sloane, N. J. A. Sequences A001037/M0116 and A005597/M4056 in "The On-Line Encyclopedia of Integer Sequences."
Wrench, J. W. "Evaluation of Artin's Constant and the Twin Prime Constant." Math. Comput. 15, 396-398, 1961.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
