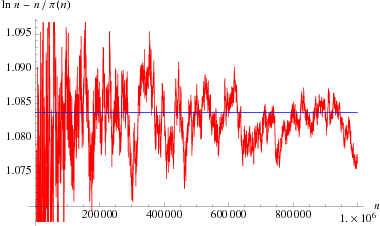
Legendre's constant is the number 1.08366 in Legendre's guess at the prime number theorem

with . Legendre first published a guess the form

in his Essai sur la Théorie des Nombres (Edwards 2001, p. 3; Havil 2003, p. 177), but in the third edition (renamed Théorie des nombres), modified it to the form above (Derbyshire 2004, pp. 55 and 369).

This expression is correct to leading term only, since it is actually true that this limit approaches 1 (Rosser and Schoenfeld 1962, Panaitopol 1999).

REFERENCES:

Abel, N. H. Letter to Holmboe. 4 August 1823. In Niels Henrik Abel, Memorial, Publié à l'Occasion du Centenaire de sa Naissance.

Chebyshev, P. L. "Sur la fonction qui détermine la totalité des nombres premiers inferieurs à une limite donnée." J. math. pures appl. 17, 1852.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Dirichlet, P. G. L. "Sur l'usage des series infinies dans la théorie des nombres." J. reine angew. Math. 18, 257-274, 1838. Reprinted in Werke, Vol. 1, pp. 359-374.

Edwards, H. M. Riemann's Zeta Function. New York: Dover, pp. 3-4, 2001.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 147, 1983.

Legendre, A. M. Essai sur la Théorie des Nombres. Paris: Duprat, 1808.

Panaitopol, L. "Several Approximations of 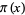." Math. Ineq. Appl. 2, 317-324, 1999.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.

Rosser, J. B. and Schoenfeld, L. "Approximate Formulas for Some Functions of Prime Numbers." Ill. J. Math. 6, 64-94, 1962.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 28-29, 1991.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جمعية كشافة الكفيل: المجالس الحسينية تعلّم الفتية قيم نهضة الإمام الحسين (عليه السلام)

عَبرَ المجالس الحسينية.. المجمَع العلمي يقدّم محاضرات دينية وتلاوات قرآنية في بغداد والنجف وميسان

برعاية العتبة العباسية المقدسة.. موكب قناديل السماء يُحيي مراسم اليوم الثالث عشر من المحرّم

بعد انتهاء مراسم ذكرى دفن الأجساد الطاهرة قسم رعاية الصحن يباشر بحملة تنظيف واسعة لصحن مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لكبح الجوع وخسارة الوزن.. "سر بسيط" في نظام جوكوفيتش ؟

هل يساعد الرجيم في علاج الأمراض العقلية؟

لحماية أسنان طفلك.. هذا الفيتامين يقلل خطر التسوس

أكل الطعام بسرعة.. طريق سريع إلى أمراض خطيرة

المزيد

الآخبار التكنلوجية

ما هي أفضل درجة حرارة لتكييف الهواء في السيارة؟

ذوبان الأنهار الجليدية يوقظ "عمالقة نائمة"!

9 يوليو يشهد أقصر يوم في التاريخ المسجل ؟!!

راتبه عشرات ملايين الدولارات.. زوكربرغ يخطف "عقل أبل"

المزيد