Machin-Like Formulas

Machin-like formulas have the form

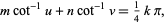(1)

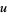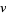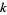where , , and  are positive integers an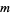d  and 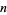 are nonnegative integers. Some such formulas can be found by converting the inverse tangent decompositions for which  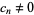in the table of Todd (1949) to inverse cotangents. However, this gives only Machin-like formulas in which the smallest term is .

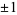Generalized Machin-like formulas in which the argument of the cotangents are rational numbers, including Euler's

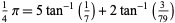(2)

(Lehmer 1938, Wetherfield 1996), square roots such as

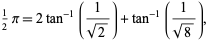(3)

or even mixed quadratic surds (Lehmer 1938) have also been considered.

A trivial one-term Machin-like formula is given by the identity

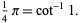(4)

Two-term Machin-like formulas can be derived by writing

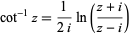(5)

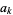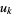and looking for  and  such that

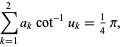(6)

so

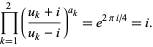(7)

Machin-like formulas exist iff (7) has a solution in integers. This is equivalent to finding positive integer values 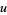, , 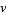and 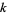 and integer values  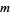and 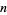 such that

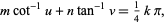(8)

which occur iff

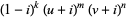(9)

is real (Borwein and Borwein 1987, p. 345). Another equivalent formulation is to find all integer solutions to one of

			(10)
			(11)

for 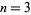, 5, ....

There are only four such two-term formulas,

			(12)
			(13)
			(14)
			(15)

known as Machin's formula (Borwein and Bailey 2003, p. 105), Euler's Machin-like formula (Borwein and Bailey 2003, p. 105), Hermann's formula, and Hutton's formula. These follow from the identities

			(16)
			(17)
			(18)
			(19)

Three-term Machin-like formulas include Gauss's Machin-like formula

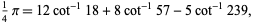(20)

Strassnitzky's formula

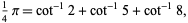(21)

which was used by Dase (Borwein and Bailey 2003, p. 106), and the following:

			(22)
			(23)
			(24)
			(25)
			(26)

The first is due to Størmer, the second due to Rutherford, and the last appears in Borwein and Bailey (2003, p. 107). However, there are many other such formulas, a total of 105 of which are tabulated by Weisstein.

A total of 90 five-term Machin-like formulas are tabulated by Weisstein, including the two given by Borwein and Bailey (2003, pp. 62 and 111)

			(27)
			(28)

the first of which was found by high school teacher K. Takano in 1982 and the second of which was known to Störmer in 1896.

Using trigonometric identities such as

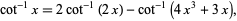(29)

it is possible to generate an infinite sequence of Machin-like formulas. Systematic searches therefore most often concentrate on formulas with particularly "nice" properties (such as "efficiency").

The efficiency of a generalized Machin-like formula (possibly with rational, quadratic surd, or other inverse cotangent arguments) is the time it takes to calculate 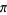 with the power series for inverse cotangent given by

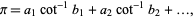(30)

and can be roughly characterized using Lehmer's "measure" formula

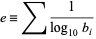(31)

(Lehmer 1938). The number of terms required to achieve a given precision is roughly proportional to 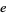, so lower 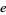-values correspond to better sums. The best currently known efficiency is 1.51244, which is achieved by the 6-term series

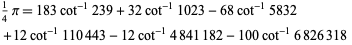(32)

discovered by C.-L. Hwang (1997). Hwang (1997) also discovered the remarkable identities

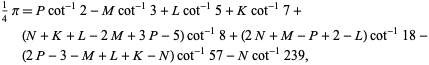(33)

where 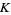, , 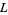, , 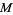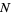and 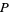 are positive integers, and

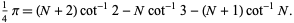(34)

The following table gives the number 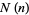 of Machin-like formulas of  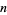terms in the compilation by Weisstein. Except for previously known identities (which are included), the criteria for inclusion are the following:

1. first term 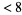 digits: measure .

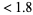2. first term = 8 digits: measure .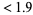

3. first term = 9 digits: measure .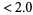

4. first term =10 digits: measure .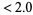

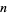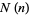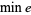1	1	0
2	4	1.85113
3	106	1.78661
4	39	1.58604
5	90	1.63485
6	120	1.51244
7	113	1.54408
8	18	1.65089
9	4	1.72801
10	78	1.63086
11	34	1.6305
12	188	1.67458
13	37	1.71934
14	5	1.75161
15	24	1.77957
16	51	1.81522
17	5	1.90938
18	570	1.87698
19	1	1.94899
20	11	1.95716
21	1	1.98938
Total	1500	1.51244

REFERENCES:

Arndt, J. "Arctan Formulas." http://www.jjj.de/hfloat/jjf.ps.

Arndt, J. "Big ArcTan Formula Bucket." http://www.jjj.de/hfloat/fox.ps.

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 347-359, 1987.

Berstel, J.; Pin, J.-E.; and Pocchiola, M. Mathématiques et informatique: Problémes résolus. New York: McGraw-Hill, 1991.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.

Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 241-248, 1996.

Gourdon, X. and Sebah, P. "Collection of Series for ." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.

Hwang, C.-L. "More Machin-Type Identities." Math. Gaz. 81, 120-121, 1997.

Lehmer, D. H. "On Arccotangent Relations for ." Amer. Math. Monthly 45, 657-664, 1938.

Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981.

Lewin, L. Structural Properties of Polylogarithms. Providence, RI: Amer. Math. Soc., 1991.

Nielsen, N. Der Euler'sche Dilogarithms. Leipzig, Germany: Halle, 1909.

Séroul, R. "Machin Formulas." §9.3 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 240-252, 2000.

Størmer, C. "Sur l'Application de la Théorie des Nombres Entiers Complexes à la Solution en Nombres Rationnels 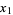, , 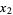..., 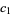, , 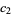...,  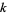de l'Equation...." Archiv for Mathematik og Naturvidenskab B 19, 75-85, 1896.

Todd, J. "A Problem on Arc Tangent Relations." Amer. Math. Monthly 56, 517-528, 1949.

Wetherfield, M. "The Enhancement of Machin's Formula by Todd's Process." Math. Gaz. 80, 333-344, 1996.

Wetherfield, M. "Machin Revisited." Math. Gaz. 81, 121-123, 1997.

Williams, R. "Arctangent Formulas for Pi." http://www.cacr.caltech.edu/~roy/upi/pi.formulas.html