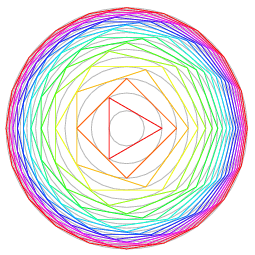
Circumscribe a triangle about a circle, another circle around the triangle, a square outside the circle, another circle outside the square, and so on. The circumradius and inradius for an 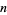-gon are then related by

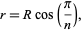(1)

so an infinitely nested set of circumscribed polygons and circles has

			(2)
			(3)
			(4)

Kasner and Newman (1989) and Haber (1964) state that 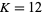, but this is incorrect, and the actual answer is

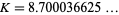(5)

(OEIS A051762).

By writing

(6)

it is possible to expand the series about infinity, change the order of summation, do the 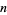 sum symbolically, and obtain the quickly converging series

{sum_(k=1)^infty((4^k-1)zeta(2k)[4^k(zeta(2k)-1)-1])/(4^kk)}, " src="http://mathworld.wolfram.com/images/equations/PolygonCircumscribing/NumberedEquation4.gif" style="height:47px; width:293px" />

(7)

where 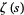 is the Riemann zeta function.

Bouwkamp (1965) produced the following infinite product formulas for the constant,

		{product_(m=1)^(infty)product_(n=1)^(infty)[1-1/(m^2(n+1/2)^2)]}^(-1)" src="http://mathworld.wolfram.com/images/equations/PolygonCircumscribing/Inline16.gif" style="height:55px; width:185px" />	(8)
			(9)
		{sum_(k=1)^(infty)([lambda(2k)-1]2^(2k)[zeta(2k)-1-2^(-2k)])/k}," src="http://mathworld.wolfram.com/images/equations/PolygonCircumscribing/Inline22.gif" style="height:47px; width:279px" />	(10)

where 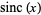 is the sinc function (cf. Prudnikov et al. 1986, p. 757),  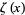is the Riemann zeta function, and  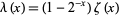is the Dirichlet lambda function. Bouwkamp (1965) also produced the formula with accelerated convergence

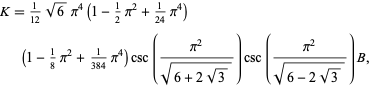(11)

where

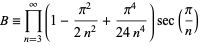(12)

(cited in Pickover 1995).

REFERENCES:

Bouwkamp, C. "An Infinite Product." Indag. Math. 27, 40-46, 1965.

Chatterji, M. "Product[Cos[Pi/n], n,3,infinity]." http://www.worldwideschool.org/library/books/sci/math/MiscellaneousMathematicalConstants/chap102.html.

Finch, S. R. "Kepler-Bouwkamp Constant." §6.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 428-429, 2003.

Haber, H. "Das Mathematische Kabinett." Bild der Wissenschaft 2, 73, Apr. 1964.

Hamming, R. W. Numerical Methods for Scientists and Engineers, 2nd ed. New York: Dover, pp. 193-194, 1986.

Kasner, E. and Newman, J. R. Mathematics and the Imagination. Redmond, WA: Microsoft Press, pp. 311-312, 1989.

Pappas, T. "Infinity & Limits." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 180, 1989.

Pickover, C. A. "Infinitely Exploding Circles." Ch. 18 in Keys to Infinity. New York: W. H. Freeman, pp. 147-151, 1995.

Pinkham, R. S. "Mathematics and Modern Technology." Amer. Math. Monthly 103, 539-545, 1996.

Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.

Sloane, N. J. A. Sequence A051762 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد