المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hard Hexagon Entropy Constant |
 877
 05:39 مساءً
date: 19-1-2020 |
Author : Baxter, R. J 
Book or Source : "Hard Hexagons: Exact Solution." J. Physics A 13 
Page and Part : ...|
Read More
Date: 20-7-2020
1141
Date: 3-3-2020
588
Date: 26-10-2020
1346
|
Consider an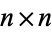 
(0, 1)-matrix such as
![[a_(11) a_(23) ; a_(22) a_(34); a_(21) a_(33) ; a_(32) a_(44); a_(31) a_(43) ; a_(42) a_(54); a_(41) a_(53) ; a_(52) a_(64)]](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/NumberedEquation1.gif) |
(1) |
for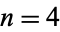 
. Call two elements 
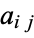adjacent if they lie in positions 
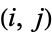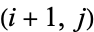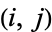and 
, 
and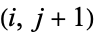 
, or 
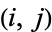and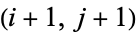 
for some 
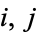. Call 
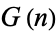the number of such arrays with no pairs of adjacent 1s. Equivalently, 
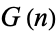is the number of configurations of nonattacking kings on an 
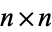chessboard with regular hexagonal cells.
The first few values of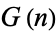 
for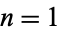 
, 2, ... are 2, 6, 43, 557, 14432, ... (OEIS A066863).
The hard square hexagon constant is then given by
 |
 |
![lim_(n->infty)[G(n)]^(1/n^2)](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline18.gif) |
(2) |
 |
 |
 |
(3) |
(OEIS A085851).
Amazingly,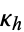 
is algebraic and is given by
 |
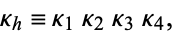(4) |
where
 |
 |
 |
(5) |
 |
 |
![[1-sqrt(1-c)+sqrt(2+c+2sqrt(1+c+c^2))]^2](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline28.gif) |
(6) |
 |
 |
![[-1-sqrt(1-c)+sqrt(2+c+2sqrt(1+c+c^2))]^2](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline31.gif) |
(7) |
 |
 |
![[sqrt(1-a)+sqrt(2+a+2sqrt(1+a+a^2))]^(-1/2)](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline34.gif) |
(8) |
 |
 |
 |
(9) |
 |
 |
 |
(10) |
 |
 |
![{1/4+3/8a[(b+1)^(1/3)-(b-1)^(1/3)]}^(1/3).](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline43.gif) |
(11) |
(Baxter 1980, Joyce 1988ab).
The variable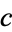 
can be expressed in terms of the tribonacci constant
 |
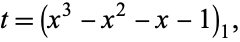(12) |
where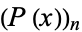 
is a polynomial root, as
 |
 |
![[1/4-(31(13t+81))/(242(32t+7))]^(1/3)](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline48.gif) |
(13) |
 |
 |
![[1/4-(31(32t^2-39t-19))/(2662)]^(1/3)](http://mathworld.wolfram.com/images/equations/HardHexagonEntropyConstant/Inline51.gif) |
(14) |
 |
 |
 |
(15) |
(T. Piezas III, pers. comm., Feb. 11, 2006).
Explicitly,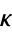 
is the unique positive root
 |
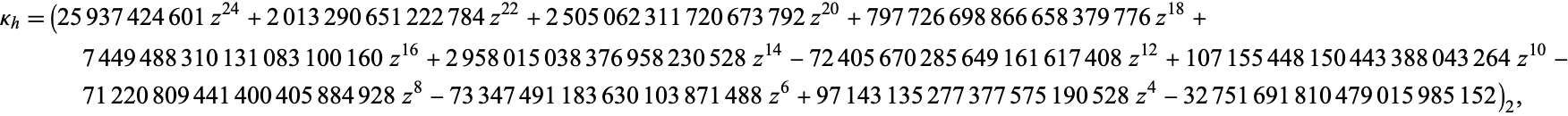(16) |
where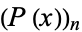 
denotes the 
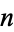th root of the polynomial 
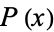in the ordering of the Wolfram Language.
REFERENCES:
Baxter, R. J. "Hard Hexagons: Exact Solution." J. Physics A 13, 1023-1030, 1980.
Baxter, R. J. Exactly Solved Models in Statistical Mechanics. New York: Academic Press, 1982.
Finch, S. R. "Hard Square Entropy Constant." §5.12 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 342-349, 2003.
Joyce, G. S. "On the Hard Hexagon Model and the Theory of Modular Functions." Phil. Trans. Royal Soc. London A 325, 643-702, 1988a.
Joyce, G. S. "Exact Results for the Activity and Isothermal Compressibility of the Hard-Hexagon Model." J. Phys. A: Math. Gen. 21, L983-L988, 1988b.
Katzenelson, J. and Kurshan, R. P. "S/R: A Language for Specifying Protocols and Other Coordinating Processes." In Proc. IEEE Conf. Comput. Comm., pp. 286-292, 1986.
Sloane, N. J. A. Sequences A066863 and A085851 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
