

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Eisenstein Series
المؤلف:
Bump, D
المصدر:
Automorphic Forms and Representations. Cambridge, England: Cambridge University Press
الجزء والصفحة:
...
22-12-2019
2486
Eisenstein Series
An Eisenstein series with half-period ratio 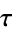 and index
and index 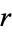 is defined by
is defined by
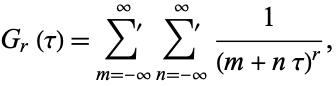 |
(1) |
where the sum 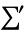 excludes
excludes 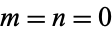 ,
, ![I[tau]>0](http://mathworld.wolfram.com/images/equations/EisensteinSeries/Inline5.gif) , and
, and 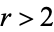 is an integer (Apostol 1997, p. 12).
is an integer (Apostol 1997, p. 12).
The Eisenstein series satisfies the remarkable property
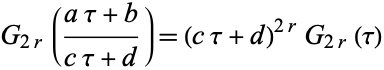 |
(2) |
if the matrix ![[a b; c d]](http://mathworld.wolfram.com/images/equations/EisensteinSeries/Inline7.gif) is in the special linear group
is in the special linear group 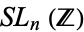 (Serre 1973, pp. 79 and 83). Therefore,
(Serre 1973, pp. 79 and 83). Therefore, 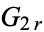 is a modular form of weight
is a modular form of weight 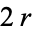 (Serre 1973, p. 83).
(Serre 1973, p. 83).
Furthermore, each Eisenstein series is expressible as a polynomial of the elliptic invariants 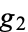 and
and 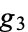 of the Weierstrass elliptic function with positive rational coefficients (Apostol 1997).
of the Weierstrass elliptic function with positive rational coefficients (Apostol 1997).
The Eisenstein series satisfy
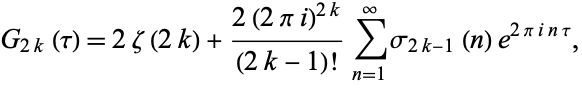 |
(3) |
where 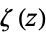 is the Riemann zeta function and
is the Riemann zeta function and 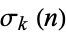 is the divisor function (Apostol 1997, pp. 24 and 69). Writing the nome
is the divisor function (Apostol 1997, pp. 24 and 69). Writing the nome 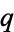 as
as
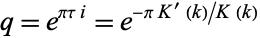 |
(4) |
where 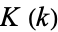 is a complete elliptic integral of the first kind,
is a complete elliptic integral of the first kind, 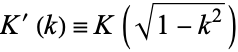 ,
, 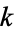 is the elliptic modulus, and defining
is the elliptic modulus, and defining
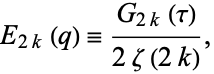 |
(5) |
we have
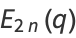 |
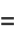 |
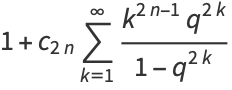 |
(6) |
 |
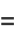 |
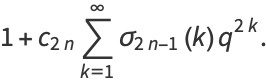 |
(7) |
where
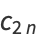 |
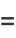 |
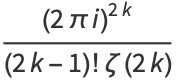 |
(8) |
 |
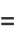 |
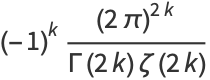 |
(9) |
 |
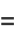 |
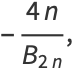 |
(10) |
where 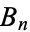 is a Bernoulli number. For
is a Bernoulli number. For 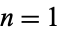 , 2, ..., the first few values of
, 2, ..., the first few values of 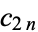 are
are 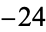 , 240,
, 240, 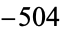 , 480, -264,
, 480, -264, 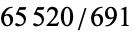 , ... (OEIS A006863 and A001067).
, ... (OEIS A006863 and A001067).
The first few values of 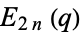 are therefore
are therefore
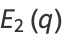 |
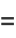 |
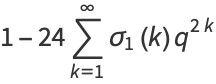 |
(11) |
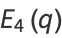 |
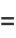 |
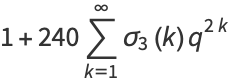 |
(12) |
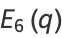 |
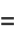 |
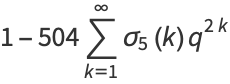 |
(13) |
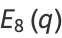 |
 |
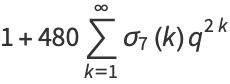 |
(14) |
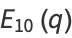 |
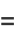 |
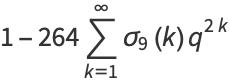 |
(15) |
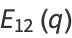 |
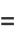 |
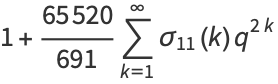 |
(16) |
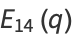 |
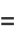 |
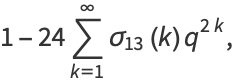 |
(17) |
(Apostol 1997, p. 139). Ramanujan used the notations 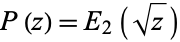 ,
, 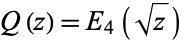 , and
, and 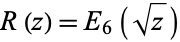 , and these functions satisfy the system of differential equations
, and these functions satisfy the system of differential equations
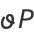 |
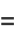 |
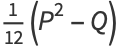 |
(18) |
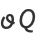 |
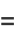 |
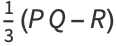 |
(19) |
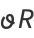 |
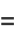 |
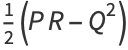 |
(20) |
(Nesterenko 1999), where 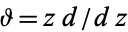 is the differential operator.
is the differential operator.
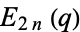 can also be expressed in terms of complete elliptic integrals of the first kind
can also be expressed in terms of complete elliptic integrals of the first kind 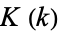 as
as
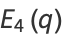 |
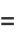 |
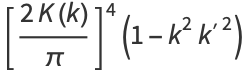 |
(21) |
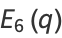 |
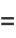 |
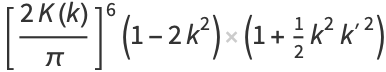 |
(22) |
(Ramanujan 1913-1914), where 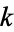 is the elliptic modulus. Ramanujan used the notation
is the elliptic modulus. Ramanujan used the notation 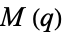 and
and 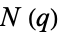 to refer to
to refer to 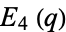 and
and 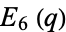 , respectively.
, respectively.
Pretty formulas are given by
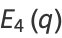 |
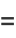 |
![1/2[theta_2^8(q)+theta_3^8(q)+theta_4^8(q)]](http://mathworld.wolfram.com/images/equations/EisensteinSeries/Inline90.gif) |
(23) |
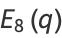 |
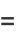 |
![1/2[theta_2^(16)(q)+theta_3^(16)(q)+theta_4^(16)(q)],](http://mathworld.wolfram.com/images/equations/EisensteinSeries/Inline93.gif) |
(24) |
where 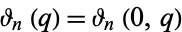 is a Jacobi theta function.
is a Jacobi theta function.
The following table gives the first few Eisenstein series 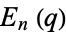 for even
for even 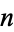 .
.
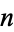 |
OEIS | lattice | 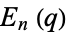 |
| 2 | A006352 | 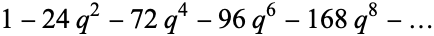 |
|
| 4 | A004009 | 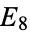 |
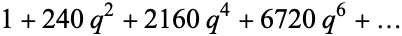 |
| 6 | A013973 | 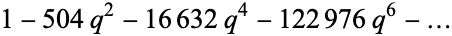 |
|
| 8 | A008410 | 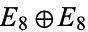 |
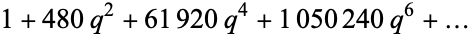 |
| 10 | A013974 | 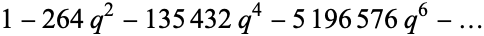 |
The notation 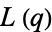 is sometimes used to refer to the closely related function
is sometimes used to refer to the closely related function
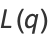 |
 |
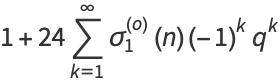 |
(25) |
 |
 |
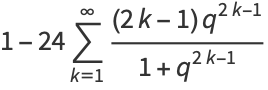 |
(26) |
 |
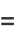 |
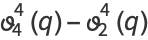 |
(27) |
 |
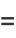 |
![[(2K(k))/pi]^2(1-2k^2)](http://mathworld.wolfram.com/images/equations/EisensteinSeries/Inline118.gif) |
(28) |
 |
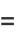 |
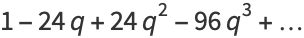 |
(29) |
(OEIS A103640), where 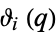 is a Jacobi elliptic function and
is a Jacobi elliptic function and
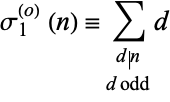 |
(30) |
is the odd divisor function (Ramanujan 2000, p. 32).
REFERENCES:
Apostol, T. M. "The Eisenstein Series and the Invariants 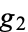 and
and 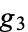 " and "The Eisenstein Series
" and "The Eisenstein Series 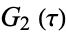 ." §1.9 and 3.10 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 12-13 and 69-71, 1997.
." §1.9 and 3.10 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 12-13 and 69-71, 1997.
Borcherds, R. E. "Automorphic Forms on 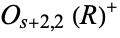 and Generalized Kac-Moody Algebras." In Proc. Internat. Congr. Math., Vol. 2. pp. 744-752, 1994.
and Generalized Kac-Moody Algebras." In Proc. Internat. Congr. Math., Vol. 2. pp. 744-752, 1994.
Borwein, J. M. and Borwein, P. B. "Class Number Three Ramanujan Type Series for 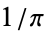 ." J. Comput. Appl. Math. 46, 281-290, 1993.
." J. Comput. Appl. Math. 46, 281-290, 1993.
Bump, D. Automorphic Forms and Representations. Cambridge, England: Cambridge University Press, p. 29, 1997.
Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, pp. 119 and 123, 1993.
Coxeter, H. S. M. "Integral Cayley Numbers."The Beauty of Geometry: Twelve Essays. New York: Dover, pp. 20-39, 1999.
Gunning, R. C. Lectures on Modular Forms. Princeton, NJ: Princeton Univ. Press, p. 53, 1962.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 166, 1999.
Milne, S. C. "Hankel Determinants of Eisenstein Series." 13 Sep 2000. http://arxiv.org/abs/math.NT/0009130.
Nesterenko, Yu. V. A Course on Algebraic Independence: Lectures at IHP 1999. Unpublished manuscript. 1999.
Ramanujan, S. "Modular Equations and Approximations to 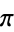 ." Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.
." Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.
Serre, J.-P. A Course in Arithmetic. New York: Springer-Verlag, 1973.
Shimura, G. Euler Products and Eisenstein Series. Providence, RI: Amer. Math. Soc., 1997.
Sloane, N. J. A. Sequences A001067, A004009/M5416, A006863/M5150, A008410, A013973, A013974, and A103640 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















