

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Dirichlet L-Series
المؤلف:
Apostol, T. M
المصدر:
Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
الجزء والصفحة:
...
19-12-2019
1629
Dirichlet L-Series
A Dirichlet 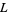 -series is a series of the form
-series is a series of the form
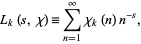 |
(1) |
where the number theoretic character 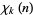 is an integer function with period
is an integer function with period 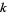 , are called Dirichlet
, are called Dirichlet 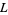 -series. These series are very important in additive number theory (they were used, for instance, to prove Dirichlet's theorem), and have a close connection with modular forms. Dirichlet
-series. These series are very important in additive number theory (they were used, for instance, to prove Dirichlet's theorem), and have a close connection with modular forms. Dirichlet 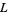 -series can be written as sums of Lerch transcendents with
-series can be written as sums of Lerch transcendents with 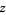 a power of
a power of 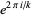 .
.
Dirichlet 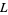 -series is implemented in the Wolfram Language as DirichletL[k, j, s] for the Dirichlet character
-series is implemented in the Wolfram Language as DirichletL[k, j, s] for the Dirichlet character 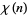 with modulus
with modulus 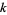 and index
and index 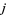 .
.
The generalized Riemann hypothesis conjectures that neither the Riemann zeta function nor any Dirichlet 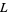 -series has a zero with real part larger than 1/2.
-series has a zero with real part larger than 1/2.
The Dirichlet lambda function
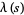 |
 |
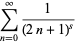 |
(2) |
 |
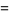 |
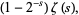 |
(3) |
Dirichlet beta function
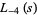 |
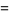 |
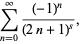 |
(4) |
 |
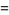 |
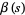 |
(5) |
and Riemann zeta function
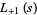 |
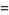 |
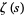 |
(6) |
 |
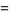 |
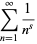 |
(7) |
are all Dirichlet 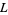 -series (Borwein and Borwein 1987, p. 289).
-series (Borwein and Borwein 1987, p. 289).
Hecke (1936) found a remarkable connection between each modular form with Fourier series
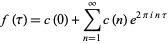 |
(8) |
and the Dirichlet 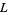 -series
-series
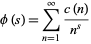 |
(9) |
This Dirichlet series converges absolutely for ![sigma=R[s]>k+1](http://mathworld.wolfram.com/images/equations/DirichletL-Series/Inline33.gif) (if
(if 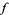 is a cusp form) and
is a cusp form) and 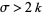 if
if 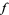 is not a cusp form. In particular, if the coefficients
is not a cusp form. In particular, if the coefficients 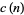 satisfy the multiplicative property
satisfy the multiplicative property
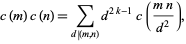 |
(10) |
then the Dirichlet 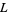 -series will have a representation of the form
-series will have a representation of the form
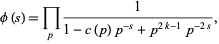 |
(11) |
which is absolutely convergent with the Dirichlet series (Apostol 1997, pp. 136-137). In addition, let 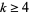 be an even integer, then
be an even integer, then 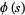 can be analytically continued beyond the line
can be analytically continued beyond the line 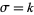 such that
such that
1. If 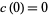 , then
, then 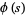 is an entire function of
is an entire function of 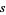 ,
,
2. If 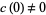 ,
, 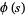 is analytic for all
is analytic for all 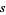 except a single simple pole at
except a single simple pole at 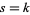 with complex residue
with complex residue
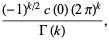 |
(12) |
where 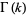 is the gamma function, and
is the gamma function, and
3. 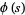 satisfies
satisfies
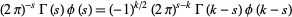 |
(13) |
(Apostol 1997, p. 137).
The number theoretic character 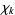 is called primitive if the j-conductor
is called primitive if the j-conductor 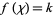 . Otherwise,
. Otherwise, 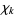 is imprimitive. A primitive
is imprimitive. A primitive 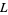 -series modulo
-series modulo 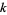 is then defined as one for which
is then defined as one for which 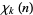 is primitive. All imprimitive
is primitive. All imprimitive 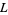 -series can be expressed in terms of primitive
-series can be expressed in terms of primitive 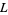 -series.
-series.
Let 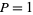 or
or 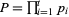 , where
, where 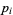 are distinct odd primes. Then there are three possible types of primitive
are distinct odd primes. Then there are three possible types of primitive 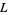 -series with real coefficients. The requirement of real coefficients restricts the number theoretic character to
-series with real coefficients. The requirement of real coefficients restricts the number theoretic character to 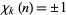 for all
for all 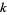 and
and 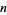 . The three type are then
. The three type are then
1. If 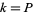 (e.g.,
(e.g., 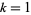 , 3, 5, ...) or
, 3, 5, ...) or 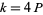 (e.g.,
(e.g., 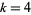 , 12, 20, ...), there is exactly one primitive
, 12, 20, ...), there is exactly one primitive 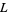 -series.
-series.
2. If 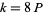 (e.g.,
(e.g., 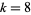 , 24, ...), there are two primitive
, 24, ...), there are two primitive 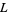 -series.
-series.
3. If 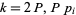 , or
, or 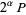 where
where 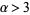 (e.g.,
(e.g., 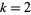 , 6, 9, ...), there are no primitive
, 6, 9, ...), there are no primitive 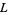 -series
-series
(Zucker and Robertson 1976). All primitive 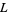 -series are algebraically independent and divide into two types according to
-series are algebraically independent and divide into two types according to
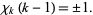 |
(14) |
Primitive 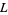 -series of these types are denoted
-series of these types are denoted 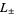 . For a primitive
. For a primitive 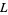 -series with real number theoretic character, if
-series with real number theoretic character, if 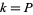 , then
, then
|
(15) |
If 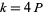 , then
, then
|
(16) |
and if 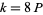 , then there is a primitive function of each type (Zucker and Robertson 1976).
, then there is a primitive function of each type (Zucker and Robertson 1976).
The first few primitive negative 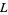 -series are
-series are 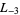 ,
, 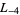 ,
, 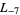 ,
, 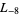 ,
, 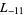 ,
, 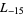 ,
, 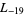 ,
, 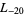 ,
, 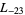 ,
, 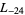 ,
, 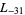 ,
, 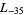 ,
, 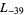 ,
, 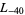 ,
, 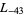 ,
, 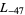 ,
, 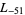 ,
, 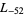 ,
, 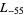 ,
, 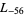 ,
, 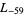 ,
, 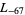 ,
, 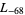 ,
, 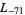 ,
, 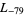 ,
, 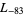 ,
, 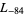 ,
, 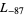 ,
, 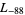 ,
, 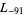 ,
, 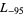 , ... (OEIS A003657), corresponding to the negated discriminants of imaginary quadratic fields. The first few primitive positive
, ... (OEIS A003657), corresponding to the negated discriminants of imaginary quadratic fields. The first few primitive positive 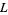 -series are
-series are 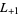 ,
, 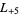 ,
, 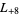 ,
, 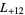 ,
, 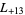 ,
, 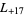 ,
, 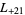 ,
, 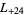 ,
, 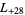 ,
, 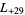 ,
, 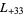 ,
, 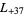 ,
, 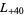 ,
, 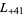 ,
, 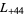 ,
, 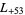 ,
, 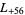 ,
, 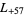 ,
, 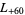 ,
, 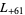 ,
, 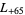 ,
, 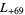 ,
, 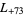 ,
, 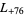 ,
, 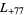 ,
, 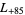 ,
, 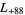 ,
, 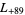 ,
, 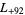 ,
, 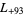 ,
, 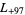 , ... (OEIS A003658).
, ... (OEIS A003658).
The Kronecker symbol 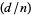 is a real number theoretic character modulo
is a real number theoretic character modulo 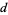 , and is in fact essentially the only type of real primitive number theoretic character mod
, and is in fact essentially the only type of real primitive number theoretic character mod 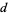 (Ayoub 1963). Therefore,
(Ayoub 1963). Therefore,
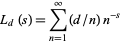 |
(17) |
where 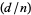 is the Kronecker symbol (Borwein and Borwein 1987, p. 293).
is the Kronecker symbol (Borwein and Borwein 1987, p. 293).
For primitive values of 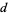 , the Kronecker symbols are periodic with period
, the Kronecker symbols are periodic with period 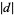 , so
, so 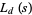 can be written in the form of
can be written in the form of 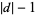 sums, each of which can be expressed in terms of the polygamma function
sums, each of which can be expressed in terms of the polygamma function 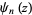 , giving
, giving
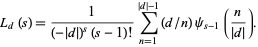 |
(18) |
The functional equations for 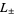 are
are
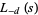 |
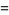 |
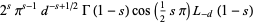 |
(19) |
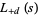 |
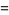 |
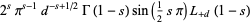 |
(20) |
(Borwein and Borwein 1986, p. 303).
For 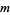 a positive integer
a positive integer
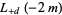 |
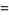 |
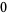 |
(21) |
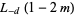 |
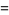 |
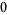 |
(22) |
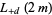 |
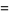 |
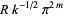 |
(23) |
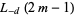 |
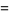 |
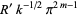 |
(24) |
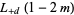 |
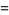 |
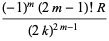 |
(25) |
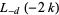 |
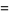 |
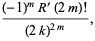 |
(26) |
where 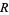 and
and 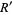 are rational numbers. Nothing general appears to be known about
are rational numbers. Nothing general appears to be known about 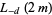 or
or 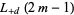 , although it is possible to express all
, although it is possible to express all 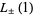 in terms of known transcendentals (Zucker and Robertson 1976).
in terms of known transcendentals (Zucker and Robertson 1976).
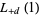 can be expressed in terms of transcendentals by
can be expressed in terms of transcendentals by
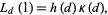 |
(27) |
where 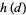 is the class number and
is the class number and 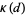 is the Dirichlet structure constant.
is the Dirichlet structure constant.
No general forms are known for 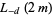 and
and 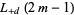 in terms of known transcendentals. Edwards (2000) gives several examples of special cases of
in terms of known transcendentals. Edwards (2000) gives several examples of special cases of 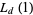 . A number of primitive series
. A number of primitive series 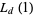 are given by
are given by
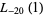 |
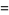 |
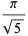 |
(28) |
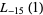 |
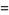 |
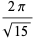 |
(29) |
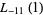 |
 |
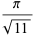 |
(30) |
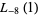 |
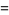 |
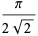 |
(31) |
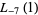 |
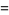 |
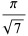 |
(32) |
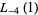 |
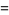 |
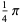 |
(33) |
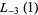 |
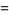 |
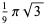 |
(34) |
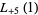 |
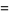 |
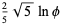 |
(35) |
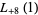 |
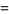 |
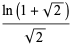 |
(36) |
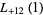 |
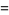 |
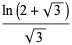 |
(37) |
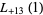 |
 |
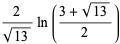 |
(38) |
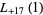 |
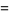 |
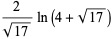 |
(39) |
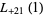 |
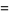 |
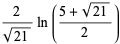 |
(40) |
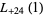 |
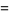 |
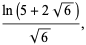 |
(41) |
and for 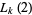 are given by
are given by
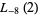 |
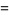 |
![1/(64)[psi_1(1/8)+psi_1(3/8)-psi_1(5/8)-psi_1(7/8)]](http://mathworld.wolfram.com/images/equations/DirichletL-Series/Inline242.gif) |
(42) |
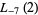 |
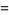 |
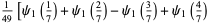 |
(43) |
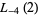 |
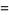 |
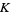 |
(44) |
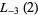 |
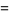 |
![1/9[psi_1(1/3)-psi_1(2/3)]](http://mathworld.wolfram.com/images/equations/DirichletL-Series/Inline251.gif) |
(45) |
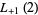 |
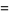 |
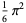 |
(46) |
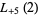 |
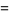 |
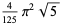 |
(47) |
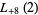 |
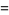 |
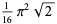 |
(48) |
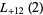 |
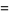 |
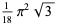 |
(49) |
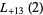 |
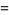 |
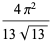 |
(50) |
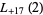 |
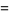 |
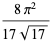 |
(51) |
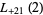 |
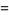 |
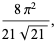 |
(52) |
where 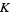 is Catalan's constant,
is Catalan's constant, 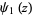 is the trigamma function, and
is the trigamma function, and 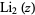 is the dilogarithm.
is the dilogarithm.
Bailey and Borwein (Bailey and Borwein 2005; Bailey et al. 2006a, pp. 5 and 62; Bailey et al. 2006b; Bailey and Borwein 2008; Coffey 2008) conjectured the relation actually in effect proved by Zagier (1986) nearly twenty years earlier (M. Coffey, pers. comm., Mar. 30, 2009) that 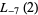 is also given by
is also given by
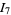 |
 |
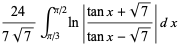 |
(53) |
 |
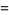 |
(54) |
|
 |
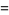 |
(55) |
|
 |
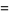 |
![4/(7sqrt(7))[3Cl_2(theta_7)-3Cl_2(2theta_7)+Cl_2(3theta_7)]](http://mathworld.wolfram.com/images/equations/DirichletL-Series/Inline288.gif) |
(56) |
 |
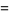 |
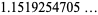 |
(57) |
where the latter expressions are due to Coffey (2008ab), with
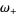 |
 |
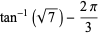 |
(58) |
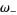 |
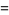 |
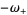 |
(59) |
 |
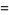 |
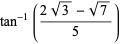 |
(60) |
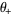 |
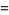 |
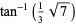 |
(61) |
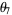 |
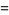 |
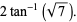 |
(62) |
REFERENCES:
Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Apostol, T. M. "Modular Forms and Dirichlet Series" and "Equivalence of Ordinary Dirichlet Series." §6.16 and §8.8 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-137 and 174-176, 1997.
Ayoub, R. G. An Introduction to the Analytic Theory of Numbers. Providence, RI: Amer. Math. Soc., 1963.
Bailey, D. H. and Borwein, J. M. "Experimental Mathematics: Examples, Methods, and Implications." Not. Amer. Math. Soc. 52, 502-514, 2005.
Bailey, D. H. and Borwein, J. M. "Computer-Assisted Discovery and Proof." In Tapas in Experimental Mathematics (Ed. T. Amdeberhan and V. Moll). Providence, RI: Amer. Math. Soc., 2008.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 222, 2006a. http://crd.lbl.gov/~dhbailey/expmath/maa-course/hyper-ema.pdf.
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006b.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Buell, D. A. "Small Class Numbers and Extreme Values of  -Functions of Quadratic Fields." Math. Comput. 139, 786-796, 1977.
-Functions of Quadratic Fields." Math. Comput. 139, 786-796, 1977.
Coffey, M. W. "Evaluation of a ln tan Integral Arising in Quantum Field Theory." J. Math. Phys. 49, 093508-1-15, 2008a.
Coffey, M. W. "Alternative Evaluation of a ln tan Integral Arising in Quantum Field Theory." Nov. 15, 2008b. http://arxiv.org/abs/0810.5077.
Edwards, H. M. Fermat's Last Theorem : A Genetic Introduction to Algebraic Number Theory. New York: Springer-Verlag, 2000.
Hecke, E. "Über die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung." Math. Ann. 112, 664-699, 1936.
Ireland, K. and Rosen, M. "Dirichlet 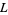 -Functions." Ch. 16 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 249-268, 1990.
-Functions." Ch. 16 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 249-268, 1990.
Koch, H. "L-Series." Ch. 7 in Number Theory: Algebraic Numbers and Functions. Providence, RI: Amer. Math. Soc., pp. 203-258, 2000.
Shanks, D. and Wrench, J. W. Jr. "The Calculation of Certain Dirichlet Series." Math. Comput. 17, 135-154, 1963.
Shanks, D. and Wrench, J. W. Jr. "Corrigendum to 'The Calculation of Certain Dirichlet Series.' " Math. Comput. 17, 488, 1963.
Sloane, N. J. A. Sequences A003657/M2332, A003658/M3776, and A103133 in "The On-Line Encyclopedia of Integer Sequences."
Zagier, D. "Hyperbolic Manifolds and Special Values of Dedekind Zeta-Functions." Invent. Math. 83, 285-301, 1986.
Zucker, I. J. and Robertson, M. M. "Some Properties of Dirichlet 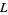 -Series." J. Phys. A: Math. Gen. 9, 1207-1214, 1976.
-Series." J. Phys. A: Math. Gen. 9, 1207-1214, 1976.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















