Archimedes' Axiom

Archimedes' axiom, also known as the continuity axiom or Archimedes' lemma, survives in the writings of Eudoxus (Boyer and Merzbach 1991), but the term was first coined by the Austrian mathematician Otto Stolz (1883). It states that, given two magnitudes having a ratio, one can find a multiple of either which will exceed the other. This principle was the basis for the method of exhaustion, which Archimedes invented to solve problems of area and volume.

Symbolically, the axiom states that

iff the appropriate one of following conditions is satisfied for integers 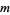 and :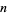

1. If 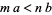, then .

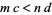2. If 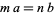, then .

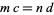3. If 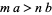, then .

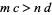Formally, Archimedes' axiom states that if 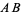 and 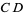 are two line segments, then there exist a finite number of points 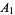, , 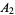...,  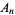on 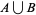 such that

and 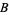 is between  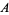and 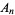 (Itô 1986, p. 611). A geometry in which Archimedes' lemma does not hold is called a non-Archimedean Geometry.

REFERENCES:

Boyer, C. B. and Merzbach, U. C. A History of Mathematics, 2nd ed. New York: Wiley, pp. 89 and 129, 1991.

Itô, K. (Ed.). §155B and 155D in Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 2. Cambridge, MA: MIT Press, p. 611, 1986.

Stolz, O. "Zur Geometrie der Alten, insbesondere über ein Axiom des Archimedes." Math. Ann. 22, 504-520, 1883.

Stolz, O. "Über das Axiom des Archimedes." Math. Ann. 39, 107-112, 1891.

Veronese, G. "Il continuo rettilineo e l'assioma cinque d'Archimede." Atti della Reale Accademia dei Lincei Ser. 4, No. 6, 603-624, 1890.