

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Inverse Cotangent
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
"Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
10-10-2019
2993
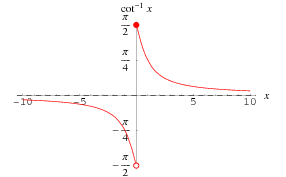
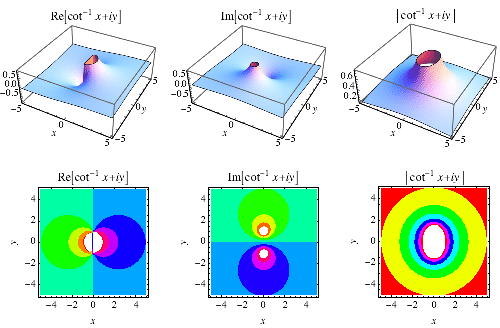
Inverse Cotangent
 |
The inverse cotangent is the multivalued function 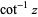 (Zwillinger 1995, p. 465), also denoted
(Zwillinger 1995, p. 465), also denoted 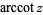 (Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 311; Jeffrey 2000, p. 124) or
(Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 311; Jeffrey 2000, p. 124) or 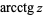 (Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 208; Jeffrey 2000, p. 127), that is the inverse function of the cotangent. The variants
(Spanier and Oldham 1987, p. 333; Gradshteyn and Ryzhik 2000, p. 208; Jeffrey 2000, p. 127), that is the inverse function of the cotangent. The variants 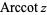 (e.g., Beyer 1987, p. 141; Bronshtein and Semendyayev, 1997, p. 70) and
(e.g., Beyer 1987, p. 141; Bronshtein and Semendyayev, 1997, p. 70) and 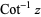 are sometimes used to refer to explicit principal values of the inverse cotangent, although this distinction is not always made (e.g., Zwillinger 1995, p. 466). Worse yet, the notation
are sometimes used to refer to explicit principal values of the inverse cotangent, although this distinction is not always made (e.g., Zwillinger 1995, p. 466). Worse yet, the notation 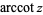 is sometimes used for the principal value, with
is sometimes used for the principal value, with 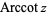 being used for the multivalued function (Abramowitz and Stegun 1972, p. 80). Note that in the notation
being used for the multivalued function (Abramowitz and Stegun 1972, p. 80). Note that in the notation 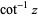 (commonly used in North America and in pocket calculators worldwide),
(commonly used in North America and in pocket calculators worldwide), 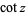 is the cotangent and the superscript
is the cotangent and the superscript 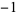 denotes an inverse function, not the multiplicative inverse.
denotes an inverse function, not the multiplicative inverse.
The principal value of the inverse cotangent is implemented in the Wolfram Language as ArcCot[z].
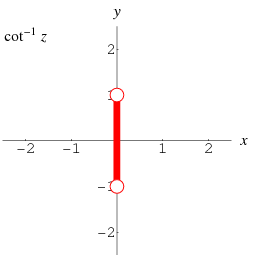
There are at least two possible conventions for defining the inverse cotangent. This work follows the convention of Abramowitz and Stegun (1972, p. 79) and the Wolfram Language, taking 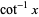 to have range
to have range ![(-pi/2,pi/2]](http://mathworld.wolfram.com/images/equations/InverseCotangent/Inline12.gif) , a discontinuity at
, a discontinuity at 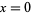 , and the branch cut placed along the line segment
, and the branch cut placed along the line segment 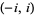 . This definition can be expressed in terms of the natural logarithm by
. This definition can be expressed in terms of the natural logarithm by
![cot^(-1)z=i/2[ln((z-i)/z)-ln((z+i)/z)].](http://mathworld.wolfram.com/images/equations/InverseCotangent/NumberedEquation1.gif) |
(1) |
This definition is also consistent, as it must be, with the Wolfram Language's definition of ArcTan, so ArcCot[z] is equal to ArcTan[1/z].
A different but common convention (e.g., Zwillinger 1995, p. 466; Bronshtein and Semendyayev, 1997, p. 70; Jeffrey 2000, p. 125) defines the range of 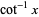 as
as 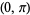 , thus giving a function that is continuous on the real line
, thus giving a function that is continuous on the real line 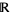 . Extreme care should be taken where examining identities involving inverse trigonometric functions, since their range of applicability or precise form may differ depending on the convention being used.
. Extreme care should be taken where examining identities involving inverse trigonometric functions, since their range of applicability or precise form may differ depending on the convention being used.
The derivative of 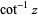 is given by
is given by
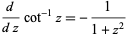 |
(2) |
and the integral by
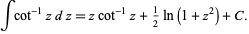 |
(3) |
The Maclaurin series of the inverse cotangent for 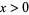 is given by
is given by
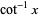 |
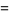 |
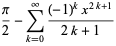 |
(4) |
 |
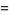 |
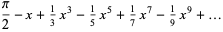 |
(5) |
(OEIS A005408). The Laurent series about 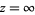 is given by
is given by
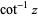 |
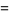 |
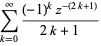 |
(6) |
 |
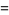 |
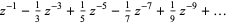 |
(7) |
for 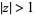 .
.
Euler derived the infinite series
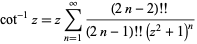 |
(8) |
(Wetherfield 1996).
The inverse cotangent satisfies
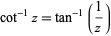 |
(9) |
for 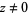 ,
,
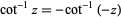 |
(10) |
for all 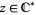 , and
, and
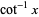 |
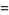 |
(11) |
|
 |
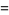 |
(12) |
|
 |
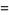 |
(13) |
|
 |
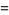 |
(14) |
|
 |
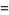 |
(15) |
|
 |
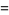 |
(16) |
|
 |
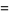 |
(17) |
Analytic sums of cotangents include the beautiful result
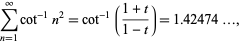 |
(18) |
(OEIS A091007), where
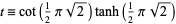 |
(19) |
(H. S. Wilf, pers. comm., May 21, 2002).
A number
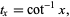 |
(20) |
where  is an integer or rational number, is sometimes called a Gregory number. Lehmer (1938a) showed that
is an integer or rational number, is sometimes called a Gregory number. Lehmer (1938a) showed that 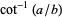 can be expressed as a finite sum of inverse cotangents of integer arguments
can be expressed as a finite sum of inverse cotangents of integer arguments
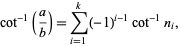 |
(21) |
where
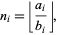 |
(22) |
with 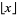 the floor function, and
the floor function, and
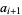 |
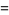 |
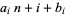 |
(23) |
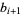 |
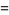 |
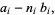 |
(24) |
with 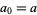 and
and 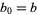 , and where the recurrence is continued until
, and where the recurrence is continued until 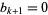 . If an inverse tangent sum is written as
. If an inverse tangent sum is written as
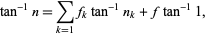 |
(25) |
then equation (◇) becomes
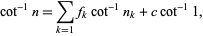 |
(26) |
where
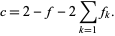 |
(27) |
Inverse cotangent sums can be used to generate Machin-like formulas.
Other inverse cotangent identities include
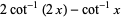 |
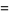 |
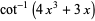 |
(28) |
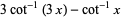 |
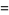 |
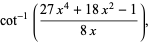 |
(29) |
as well as many others (Bennett 1926, Lehmer 1938b). Note that for equation (29), the choice of convention for 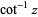 is significant, since it holds for all complex
is significant, since it holds for all complex 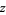 in the
in the ![[0,pi]](http://mathworld.wolfram.com/images/equations/InverseCotangent/Inline77.gif) convention, but holds only outside a lens-shaped region centered on the origin in the
convention, but holds only outside a lens-shaped region centered on the origin in the ![[-pi/2,pi/2]](http://mathworld.wolfram.com/images/equations/InverseCotangent/Inline78.gif) convention.
convention.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.
Bennett, A. A. "The Four Term Diophantine Arccotangent Relation." Ann. Math. 27, 21-24, 1926.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, p. 70, 1997.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988a.
Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61, 148-163, 1988b.
Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 311, 1998.
Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.
Lehmer, D. H. "A Cotangent Analogue of Continued Fractions." Duke Math. J. 4, 323-340, 1938a.
Lehmer, D. H. "On Arccotangent Relations for 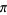 ." Amer. Math. Monthly 45, 657-664, 1938b.
." Amer. Math. Monthly 45, 657-664, 1938b.
Sloane, N. J. A. Sequences A005408/M2400 and A091007 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Wetherfield, M. "The Enhancement of Machin's Formula by Todd's Process." Math. Gaz. 80, 333-344, 1996.
Zwillinger, D. (Ed.). "Inverse Circular Functions." §6.3 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 465-467, 1995.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















