Nested Radical
Expressions of the form
 |
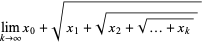(1)
|
are called nested radicals. Herschfeld (1935) proved that a nested radical of real nonnegative terms converges iff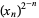 
is bounded. He also extended this result to arbitrary powers (which include continued square roots and continued fractions as well), a result is known as Herschfeld's convergence theorem.
Nested radicals appear in the computation of pi,
 |
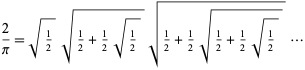(2)
|
(Vieta 1593; Wells 1986, p. 50; Beckmann 1989, p. 95), in trigonometrical values of cosine and sine for arguments of the form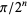 
, e.g.,
Nest radicals also appear in the computation of the golden ratio
 |
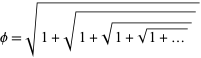(7)
|
and plastic constant
![P=RadicalBox[<span style=]() {1, +, RadicalBox[{1, +, RadicalBox[{1, +, ...}, 3]}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation4.gif" style="height:44px; width:164px" /> |
(8)
|
Both of these are special cases of
![x=RadicalBox[<span style=]() {a, +, RadicalBox[{a, +, ...}, n]}, n], " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation5.gif" style="height:26px; width:120px" /> |
(9)
|
which can be exponentiated to give
![x^n=a+RadicalBox[<span style=]() {a, +, RadicalBox[{a, +, ...}, n]}, n], " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation6.gif" style="height:26px; width:148px" /> |
(10)
|
so solutions are
 |
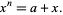(11)
|
In particular, for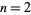 
, this gives
 |
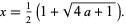(12)
|
The silver constant is related to the nested radical expression
![RadicalBox[<span style=]() {7, +, 7, RadicalBox[{7, +, ...}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation9.gif" style="height:26px; width:106px" /> |
(13)
|
There are a number of general formula for nested radicals (Wong and McGuffin). For example,
![x=RadicalBox[<span style=]() {{(, {1, -, q}, )}, {x, ^, n}, +, q, {x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{(, {1, -, q}, )}, {x, ^, n}, +, q, {x, ^, {(, {n, -, 1}, )}}, RadicalBox[..., n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation10.gif" style="height:44px; width:302px" /> |
(14)
|
which gives as special cases
 |
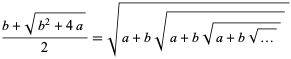(15)
|
(
, 
, 
),
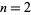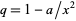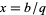![x=RadicalBox[<span style=]() {{x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{x, ^, {(, {n, -, 1}, )}}, RadicalBox[{{x, ^, {(, {n, -, 1}, )}}, RadicalBox[..., n]}, n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation12.gif" style="height:59px; width:193px" /> |
(16)
|
(
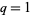), and
 |
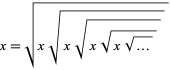(17)
|
(
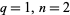). Equation (14) also gives rise to
![q^((n^k-1)/(n-1))x^(n^j)=RadicalBox[<span style=]() {{q, ^, {(, {{(, {{n, ^, {(, {k, +, 1}, )}}, -, n}, )}, /, {(, {n, -, 1}, )}}, )}}, {(, {1, -, q}, )}, {x, ^, {(, {n, ^, {(, {j, +, 1}, )}}, )}}, +, ...}, n]
...+RadicalBox[{{q, ^, {(, {{(, {{n, ^, {(, {k, +, 2}, )}}, -, n}, )}, /, {(, {n, -, 1}, )}}, )}}, {(, {1, -, q}, )}, {x, ^, {(, {n, ^, {(, {j, +, 2}, )}}, )}}, +, RadicalBox[..., n]}, n]^_, " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation14.gif" style="height:101px; width:299px" /> |
(18)
|
which gives the special case for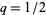 
, 
, 
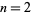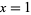, and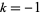 
,
 |
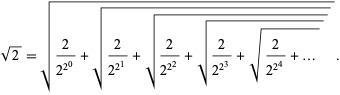(19)
|
Equation (◇) can be generalized to
![x^(1/(n-1))=RadicalBox[<span style=]() {x, RadicalBox[{x, RadicalBox[{x, ...}, n]}, n]}, n] " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation16.gif" style="height:44px; width:153px" /> |
(20)
|
for integers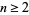 
, which follows from
In particular, taking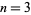 
gives
![sqrt(x)=RadicalBox[<span style=]() {x, RadicalBox[{x, RadicalBox[{x, ...}, 3]}, 3]}, 3]. " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation17.gif" style="height:44px; width:142px" /> |
(26)
|
(J. R. Fielding, pers. comm., Oct. 8, 2002).
Ramanujan discovered
 |
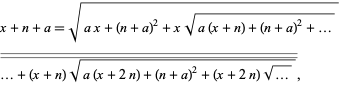(27)
|
which gives the special cases
 |
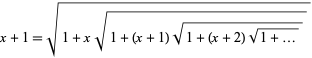(28)
|
for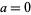 
, 
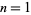(Ramanujan 1911; Ramanujan 2000, p. 323; Pickover 2002, p. 310), and
 |
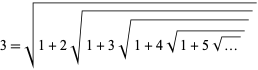(29)
|
for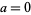 
, 
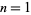, and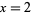 
. The justification of this process in general (and in the particular example of 
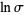, where 
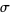is Somos's quadratic recurrence constant) is given by Vijayaraghavan (in Ramanujan 2000, p. 348).
An amusing nested radical follows rewriting the series for e
 |
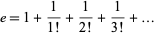(30)
|
as
 |
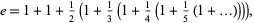(31)
|
so
![x^(e-2)=sqrt(xRadicalBox[<span style=]() {x, RadicalBox[{x, RadicalBox[{x, ...}, 5]}, 4]}, 3]) " src="http://mathworld.wolfram.com/images/equations/NestedRadical/NumberedEquation23.gif" style="height:59px; width:168px" /> |
(32)
|
(J. R. Fielding, pers. comm., May 15, 2002).
REFERENCES:
Beckmann, P. A History of Pi, 3rd ed. New York: Dorset Press, 1989.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 14-20, 1994.
Borwein, J. M. and de Barra, G. "Nested Radicals." Amer. Math. Monthly 98, 735-739, 1991.
Herschfeld, A. "On Infinite Radicals." Amer. Math. Monthly 42, 419-429, 1935.
Jeffrey, D. J. and Rich, A. D. In Computer Algebra Systems (Ed. M. J. Wester). Chichester, England: Wiley, 1999.
Landau, S. "A Note on 'Zippel Denesting.' " J. Symb. Comput. 13, 31-45, 1992a.
Landau, S. "Simplification of Nested Radicals." SIAM J. Comput. 21, 85-110, 1992b.
Landau, S. "How to Tangle with a Nested Radical." Math. Intell. 16, 49-55, 1994.
Landau, S. "
: Four Different Views." Math. Intell. 20, 55-60, 1998.
Pólya, G. and Szegö, G. Problems and Theorems in Analysis, Vol. 1. New York: Springer-Verlag, 1997.
Ramanujan, S. Question No. 298. J. Indian Math. Soc. 1911.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 327, 2000.
Sizer, W. S. "Continued Roots." Math. Mag. 59, 23-27, 1986.
Vieta, F. Uriorum de rebus mathematicis responsorum. Liber VII. 1593. Reprinted in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.
Wong, B. and McGuffin, M. "The Museum of Infinite Nested Radicals." http://www.dgp.toronto.edu/~mjmcguff/math/nestedRadicals.html.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
