q-Saalschütz Sum

A 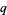-analog of the Saalschütz theorem due to Jackson is given by

where 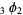 is the q-hypergeometric function (Koepf 1998, p. 40; Schilling and Warnaar 1999).

REFERENCES:

Andrews, G. E. Encyclopedia of Mathematics and Its Applications, Vol. 2: The Theory of Partitions. Cambridge, England: Cambridge University Press, 1984.

Bailey, W. N. "The Analogue of Saalschütz's Theorem." §8.4 in Generalised Hypergeometric Series. Cambridge, England: University Press, p. 68, 1935.

Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, p. 30, 1995.

Carlitz, L. "Remark on a Combinatorial Identity." J. Combin. Th. Ser. A 17, 256-257, 1974.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 13, 1990.

Gould, H. W. "A New Symmetrical Combinatorial Identity." J. Combin. Th. Ser. A 13, 278-286, 1972.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 25-26, 1998.

Schilling A. and Warnaar, S. O. "A Generalization of the q.-Saalschütz Sum and the Burge Transform" 8 Sep 1999. http://arxiv.org/abs/math.QA/9909044.

Watson, G. N. "A New Proof of the Rogers-Ramanujan Identities." J. London Math. Soc. 4, 4-9, 1929.