
Dilogarithm
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
"Dilogarithm." §27.7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
المصدر:
"Dilogarithm." §27.7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
 الجزء والصفحة:
...
الجزء والصفحة:
...
 9-8-2019
9-8-2019
 3255
3255
Dilogarithm
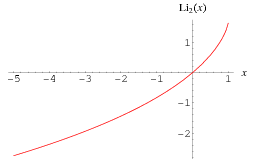
The dilogarithm 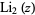 is a special case of the polylogarithm
is a special case of the polylogarithm 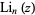 for
for 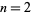 . Note that the notation
. Note that the notation 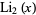 is unfortunately similar to that for the logarithmic integral
is unfortunately similar to that for the logarithmic integral 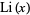 . There are also two different commonly encountered normalizations for the
. There are also two different commonly encountered normalizations for the 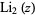 function, both denoted
function, both denoted 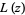 , and one of which is known as the Rogers L-function.
, and one of which is known as the Rogers L-function.
The dilogarithm is implemented in the Wolfram Language as PolyLog[2, z].
The dilogarithm can be defined by the sum
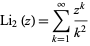 |
(1)
|
or the integral
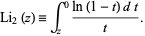 |
(2)
|
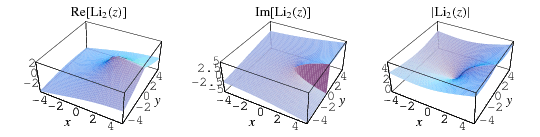
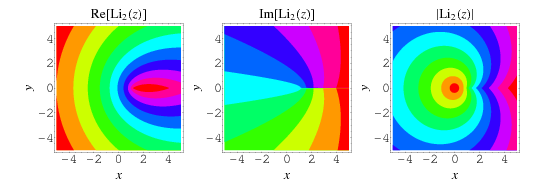
Plots of 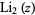 in the complex plane are illustrated above.
in the complex plane are illustrated above.
The major functional equations for the dilogarithm are given by
A complete list of 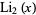 which can be evaluated in closed form is given by
which can be evaluated in closed form is given by
where  is the golden ratio (Lewin 1981, Bailey et al. 1997; Borwein et al. 2001).
is the golden ratio (Lewin 1981, Bailey et al. 1997; Borwein et al. 2001).
There are several remarkable identities involving the dilogarithm function. Ramanujan gave the identities
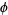 |
(20)
|
 |
(21)
|
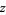 |
(22)
|
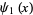 |
(23)
|
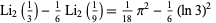 |
(24)
|
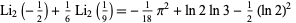 |
(25)
|
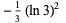 |
(26)
|
(Berndt 1994, Gordon and McIntosh 1997) in addition to the identity for 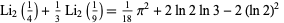 , and Bailey et al. (1997) showed that
, and Bailey et al. (1997) showed that
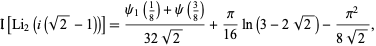 |
(27)
|
Lewin (1991) gives 67 dilogarithm identities (known as "ladders"), and Bailey and Broadhurst (1999, 2001) found the amazing additional dilogarithm identity
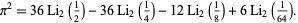 |
(28)
|
where 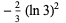 is the largest positive root of the polynomial in Lehmer's Mahler measure problem and
is the largest positive root of the polynomial in Lehmer's Mahler measure problem and 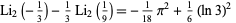 is the Riemann zeta function.
is the Riemann zeta function.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Dilogarithm." §27.7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 1004-1005, 1972.
Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Bailey, D. H. and Broadhurst, D. J. "A Seventeenth-Order Polylogarithm Ladder." 20 Jun 1999. http://arxiv.org/abs/math.CA/9906134.
Bailey, D. H. and Broadhurst, D. J. "Parallel Integer Relation Detection: Techniques and Applications." Math. Comput. 70, 1719-1736, 2001.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 323-326, 1994.
Borwein, J. M.; Bradley, D. M.; Broadhurst, D. J.; and Lisonek, P. "Special Values of Multidimensional Polylogarithms." Trans. Amer. Math. Soc. 353, 907-941, 2001.
Bytsko, A. G. "Fermionic Representations for Characters of 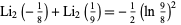 ,
, 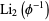 ,
, 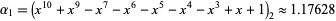 and
and 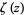 Minimal Models and Related Dilogarithm and Rogers-Ramanujan-Type Identities." J. Phys. A: Math. Gen. 32, 8045-8058, 1999.
Minimal Models and Related Dilogarithm and Rogers-Ramanujan-Type Identities." J. Phys. A: Math. Gen. 32, 8045-8058, 1999.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "Euler's Dilogarithm." §1.11.1 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 31-32, 1981.
Gordon, B. and McIntosh, R. J. "Algebraic Dilogarithm Identities." Ramanujan J. 1, 431-448, 1997.
Kirillov, A. N. "Dilogarithm Identities." Progr. Theor. Phys. Suppl. 118, 61-142, 1995.
Lewin, L. Dilogarithms and Associated Functions. London: Macdonald, 1958.
Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981.
Lewin, L. "The Dilogarithm in Algebraic Fields." J. Austral. Math. Soc. Ser. A 33, 302-330, 1982.
Lewin, L. (Ed.). Structural Properties of Polylogarithms. Providence, RI: Amer. Math. Soc., 1991.
Nielsen, N. "Der Eulersche Dilogarithmus und seine Verallgemeinerungen." Nova Acta Leopoldina, Abh. der Kaiserlich Leopoldinisch-Carolinischen Deutschen Akad. der Naturforsch. 90, 121-212, 1909.
Watson, G. N. "A Note on Spence's Logarithmic Transcendent." Quart. J. Math. Oxford Ser. 8, 39-42, 1937.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


