du Bois-Reymond Constants
المؤلف:
Finch, S. R.
المصدر:
"Du Bois Reymond,s Constants." §3.12 in Mathematical Constants. Cambridge, England: Cambridge University Press,
الجزء والصفحة:
...
30-7-2019
2506
du Bois-Reymond Constants
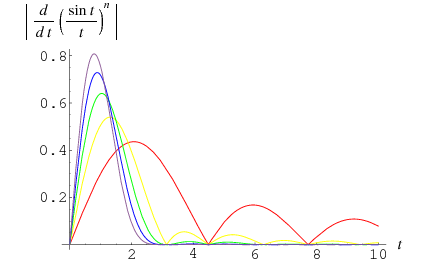
The constants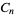 
defined by
![C_n=[int_0^infty|d/(dt)((sint)/t)^n|dt]-1.](http://mathworld.wolfram.com/images/equations/duBois-ReymondConstants/NumberedEquation1.gif) |
(1)
|
These constants can also be written as the sums
 |
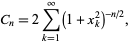(2)
|
and
![C_n=2sum_(k=1)^infty[sinc(x_k)]^n](http://mathworld.wolfram.com/images/equations/duBois-ReymondConstants/NumberedEquation3.gif) |
(3)
|
(E. Weisstein, Feb. 3, 2015), where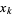 
is the 
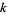th positive root of
 |
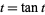(4)
|
and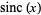 
is the sinc function.
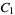diverges, with the first few subsequent constant numerically given by
Rather surprisingly, the even-ordered du Bois Reymond constants (and, in particular,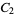 
; Le Lionnais 1983) can be computed analytically as polynomials in 
,
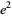(OEIS A085466 and A085467) as found by Watson (1933). For positive integer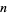 
, these have the explicit formula
![C_(2n)=-(3+delta_(1n))-2Res_(x=i)[(x^2)/((1+x^2)^n(tanx-x))],](http://mathworld.wolfram.com/images/equations/duBois-ReymondConstants/NumberedEquation5.gif) |
(11)
|
where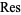 
denotes a complex residue and 
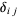is a Kronecker delta (V. Adamchik).
REFERENCES:
Finch, S. R. "Du Bois Reymond's Constants." §3.12 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 237-240, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 23, 1983.
Sloane, N. J. A. Sequences A085466 and A085467 in "The On-Line Encyclopedia of Integer Sequences."
Watson, G. N. "Du Bois Reymond's Constants." Quart. J. ath. 4, 140-146, 1933.
Young, R. M. "A Rayleigh Popular Problem." Amer. Math. Monthly 93, 660-664, 1986.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
