

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Hyperbolic Functions
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
3-6-2019
4446
Hyperbolic Functions
The hyperbolic functions 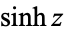 ,
, 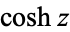 ,
, 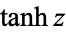 ,
, 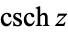 ,
, 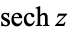 ,
, 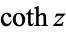 (hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cosecant, hyperbolic secant, and hyperbolic cotangent) are analogs of the circular functions, defined by removing
(hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cosecant, hyperbolic secant, and hyperbolic cotangent) are analogs of the circular functions, defined by removing 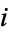 s appearing in the complex exponentials. For example,
s appearing in the complex exponentials. For example,
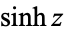 ,
, 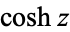 ,
, 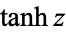 ,
, 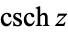 ,
, 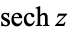 ,
, 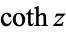 (hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cosecant, hyperbolic secant, and hyperbolic cotangent) are analogs of the circular functions, defined by removing
(hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cosecant, hyperbolic secant, and hyperbolic cotangent) are analogs of the circular functions, defined by removing 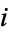 s appearing in the complex exponentials. For example,
s appearing in the complex exponentials. For example,
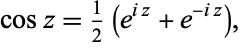 |
(1) |
so
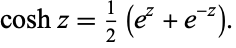 |
(2) |
Note that alternate notations are sometimes used, as summarized in the following table.
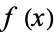 |
alternate notations |
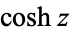 |
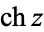 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
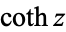 |
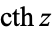 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
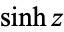 |
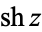 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
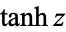 |
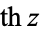 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
The hyperbolic functions share many properties with the corresponding circular functions. In fact, just as the circle can be represented parametrically by
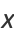 |
 |
 |
(3) |
 |
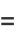 |
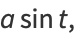 |
(4) |
a rectangular hyperbola (or, more specifically, its right branch) can be analogously represented by
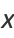 |
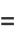 |
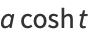 |
(5) |
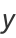 |
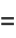 |
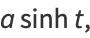 |
(6) |
where 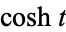 is the hyperbolic cosine and
is the hyperbolic cosine and 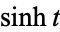 is the hyperbolic sine.
is the hyperbolic sine.
The hyperbolic functions arise in many problems of mathematics and mathematical physics in which integrals involving 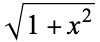 arise (whereas the circular functions involve
arise (whereas the circular functions involve 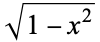 ). For instance, the hyperbolic sine arises in the gravitational potential of a cylinder and the calculation of the Roche limit. The hyperbolic cosine function is the shape of a hanging cable (the so-called catenary). The hyperbolic tangent arises in the calculation of and rapidity of special relativity. All three appear in the Schwarzschild metric using external isotropic Kruskal coordinates in general relativity. The hyperbolic secant arises in the profile of a laminar jet. The hyperbolic cotangent arises in the Langevin function for magnetic polarization.
). For instance, the hyperbolic sine arises in the gravitational potential of a cylinder and the calculation of the Roche limit. The hyperbolic cosine function is the shape of a hanging cable (the so-called catenary). The hyperbolic tangent arises in the calculation of and rapidity of special relativity. All three appear in the Schwarzschild metric using external isotropic Kruskal coordinates in general relativity. The hyperbolic secant arises in the profile of a laminar jet. The hyperbolic cotangent arises in the Langevin function for magnetic polarization.
The hyperbolic functions are defined by
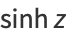 |
 |
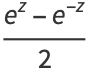 |
(7) |
 |
 |
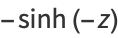 |
(8) |
 |
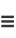 |
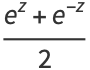 |
(9) |
 |
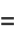 |
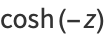 |
(10) |
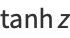 |
 |
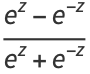 |
(11) |
 |
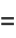 |
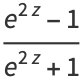 |
(12) |
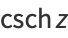 |
 |
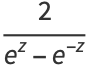 |
(13) |
 |
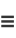 |
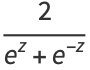 |
(14) |
 |
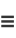 |
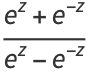 |
(15) |
 |
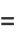 |
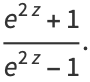 |
(16) |
For arguments multiplied by 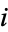 ,
,
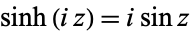 |
(17) |
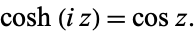 |
(18) |
The hyperbolic functions satisfy many identities analogous to the trigonometric identities (which can be inferred using Osborn's rule) such as
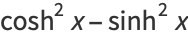 |
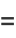 |
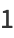 |
(19) |
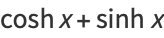 |
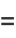 |
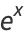 |
(20) |
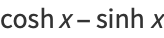 |
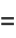 |
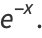 |
(21) |
See also Beyer (1987, p. 168).
Some half-angle formulas are
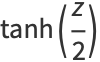 |
 |
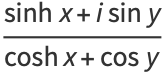 |
(22) |
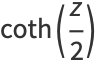 |
 |
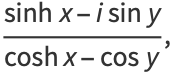 |
(23) |
where 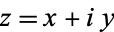 .
.
Some double-angle formulas are
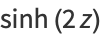 |
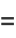 |
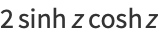 |
(24) |
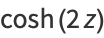 |
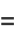 |
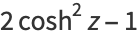 |
(25) |
 |
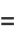 |
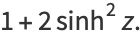 |
(26) |
Identities for complex arguments include
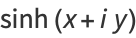 |
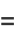 |
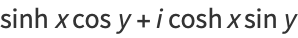 |
(27) |
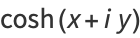 |
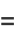 |
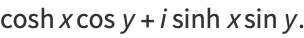 |
(28) |
The absolute squares for complex arguments are
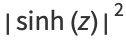 |
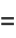 |
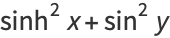 |
(29) |
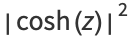 |
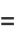 |
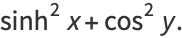 |
(30) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.
Anderson, J. W. "Trigonometry in the Hyperbolic Plane." §5.7 in Hyperbolic Geometry. New York: Springer-Verlag, pp. 146-151, 1999.
Beyer, W. H. "Hyperbolic Function." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 168-186 and 219, 1987.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 126-131, 1967.
Harris, J. W. and Stocker, H. "Hyperbolic Functions." Handbook of Mathematics and Computational Science. New York: Springer-Verlag, pp. 245-262, 1998.
Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.
Yates, R. C. "Hyperbolic Functions." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 113-118, 1952.
Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















