Factorial Sums
The sum-of-factorial powers function is defined by
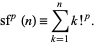 |
(1)
|
For 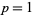 ,
,
where 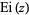 is the exponential integral,
is the exponential integral, 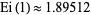 (OEIS A091725),
(OEIS A091725), 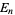 is the En-function,
is the En-function, ![R[z]](http://mathworld.wolfram.com/images/equations/FactorialSums/Inline14.gif) is the real partof
is the real partof 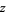 , and i is the imaginary number. The first few values are 1, 3, 9, 33, 153, 873, 5913, 46233, 409113, ... (OEIS A007489).
, and i is the imaginary number. The first few values are 1, 3, 9, 33, 153, 873, 5913, 46233, 409113, ... (OEIS A007489). 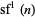 cannot be written as a hypergeometric term plus a constant (Petkovšek et al. 1996). The only prime of this form is
cannot be written as a hypergeometric term plus a constant (Petkovšek et al. 1996). The only prime of this form is 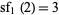 , since
, since
is always a multiple of 3 for 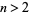 .
.
In fact, 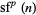 is divisible by 3 for
is divisible by 3 for 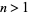 and
and 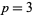 , 5, 7, ... (since the Cunningham number given by the sum of the first two terms
, 5, 7, ... (since the Cunningham number given by the sum of the first two terms 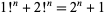 is always divisible by 3--as are all factorial powers in subsequent terms
is always divisible by 3--as are all factorial powers in subsequent terms 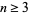 ) and so contains no primes, meaning sequences with even
) and so contains no primes, meaning sequences with even 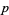 are the only prime contenders.
are the only prime contenders.
The sum
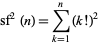 |
(8)
|
does not appear to have a simple closed form, but its values for 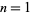 , 2, ... are 1, 5, 41, 617, 15017, 533417, 25935017, ... (OEIS A104344). It is prime for indices 2, 3, 4, 5, 7, 8, 10, 18, 21, 42, 51, 91, 133, 177, 182, 310, 3175, 9566, 32841, ... (OEIS A100289). Since
, 2, ... are 1, 5, 41, 617, 15017, 533417, 25935017, ... (OEIS A104344). It is prime for indices 2, 3, 4, 5, 7, 8, 10, 18, 21, 42, 51, 91, 133, 177, 182, 310, 3175, 9566, 32841, ... (OEIS A100289). Since 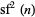 is divisible by 1248829 for
is divisible by 1248829 for 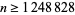 , there can be only a finite number of such primes. (However, the largest such prime is not known, which is not surprising given that
, there can be only a finite number of such primes. (However, the largest such prime is not known, which is not surprising given that 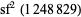 has more than 14 million decimal digits.)
has more than 14 million decimal digits.)
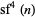 is divisible by 13 for
is divisible by 13 for 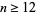 and the only prime with
and the only prime with 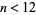 is
is 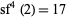 .
.
The case of 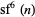 is slightly more interesting, but
is slightly more interesting, but 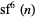 is divisible by 1091 for
is divisible by 1091 for 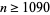 and checking the terms below that gives the only prime terms as
and checking the terms below that gives the only prime terms as 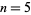 , 34, and 102 (OEIS A289947).
, 34, and 102 (OEIS A289947).
The only prime in 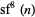 is for
is for 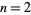 since
since 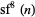 is divisible by 13 for
is divisible by 13 for 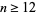 .
.
Similarly, the only primes in 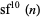 are for
are for 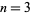 , 4, 5, 16, and 25 (OEIS A290014). since
, 4, 5, 16, and 25 (OEIS A290014). since 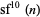 is divisible by 41 for
is divisible by 41 for 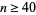 .
.
The sequence of smallest (prime) numbers 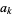 such that
such that 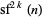 is divisible by
is divisible by 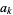 for
for 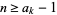 is given for
is given for 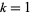 , 2, ... by 1248829, 13, 1091, 13, 41, 37, 463, 13, 23, 13, 1667, 37, 23, 13, 41, 13, 139, ... (OEIS A290250).
, 2, ... by 1248829, 13, 1091, 13, 41, 37, 463, 13, 23, 13, 1667, 37, 23, 13, 41, 13, 139, ... (OEIS A290250).
The related sum with index running from 0 instead of 1 is sometimes denoted 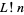 (not to be confused with the subfactorial) and known as the left factorial,
(not to be confused with the subfactorial) and known as the left factorial,
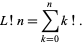 |
(9)
|
The related sum with alternating terms is known as the alternating factorial,
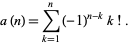 |
(10)
|
The sum
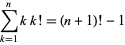 |
(11)
|
has a simple form, with the first few values being 1, 5, 23, 119, 719, 5039, ... (OEIS A033312).
Identities satisfied by sums of factorials include
(OEIS A001113, A068985, A070910, A091681, A073743, A049470, A073742, and A049469; Spanier and Oldham 1987), where 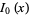 is a modified Bessel function of the first kind,
is a modified Bessel function of the first kind, 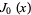 is a Bessel function of the first kind,
is a Bessel function of the first kind, 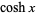 is the hyperbolic cosine,
is the hyperbolic cosine, 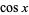 is the cosine,
is the cosine, 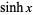 is the hyperbolic sine, and
is the hyperbolic sine, and 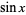 is the sine.
is the sine.
Sums of factorial powers include
(OEIS A091682 and A091683) and, in general,
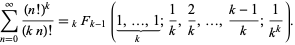 |
(24)
|
Schroeppel and Gosper (1972) give the integral representation
![sum_(n=0)^infty((n!)^3)/((3n)!)=int_0^1[P(t)+Q(t)cos^(-1)R(t)]dt,](http://mathworld.wolfram.com/images/equations/FactorialSums/NumberedEquation7.gif) |
(25)
|
where
There are only four integers equal to the sum of the factorials of their digits. Such numbers are called factorions.
While no factorial greater than 1! is a square number, D. Hoey listed sums 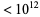 of distinct factorials which give square numbers, and J. McCranie gave the one additional sum less than
of distinct factorials which give square numbers, and J. McCranie gave the one additional sum less than 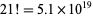 :
:
and
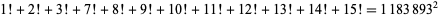 |
(43)
|
(OEIS A014597).
Sums with powers of an index in the numerator and products of factorials in the denominator can often be done analytically in terms of regularized hypergeometric functions 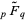 , for example
, for example
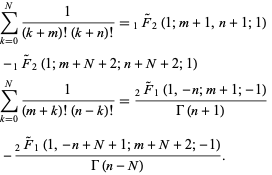 |
(44)
|
REFERENCES:
Guy, R. K. "Equal Products of Factorials," "Alternating Sums of Factorials," and "Equations Involving Factorial 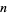 ." §B23, B43, and D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, and 193-194, 1994.
." §B23, B43, and D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, and 193-194, 1994.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Schroeppel, R. and Gosper, R. W. Item 116 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 54, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/series.html#item116.
Sloane, N. J. A. Sequences A001113/M1727, A007489/M2818, A014597, A033312, A049469, A049470, A068985, A070910, A073742, A073743, A091681, A091682, A091683, A091725, A100289, A104344, and A290250 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Factorial Function 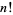 and Its Reciprocal." Ch. 2 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.
and Its Reciprocal." Ch. 2 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


