

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Factorial
المؤلف:
Boros, G. and Moll, V.
المصدر:
Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
الجزء والصفحة:
...
15-5-2019
2638
Factorial
The factorial 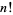 is defined for a positive integer
is defined for a positive integer 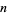 as
as
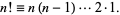 |
(1) |
So, for example, 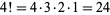 . An older notation for the factorial was written
. An older notation for the factorial was written 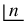 (Mellin 1909; Lewin 1958, p. 19; Dudeney 1970; Gardner 1978; Conway and Guy 1996).
(Mellin 1909; Lewin 1958, p. 19; Dudeney 1970; Gardner 1978; Conway and Guy 1996).
The special case 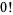 is defined to have value
is defined to have value 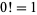 , consistent with the combinatorial interpretation of there being exactly one way to arrange zero objects (i.e., there is a single permutation of zero elements, namely the empty set
, consistent with the combinatorial interpretation of there being exactly one way to arrange zero objects (i.e., there is a single permutation of zero elements, namely the empty set 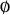 ).
).
The factorial is implemented in the Wolfram Language as Factorial[n] or n!.
The triangular number 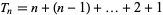 can be regarded as the additive analog of the factorial
can be regarded as the additive analog of the factorial 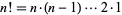 . Another relationship between factorials and triangular numbers is given by the identity
. Another relationship between factorials and triangular numbers is given by the identity
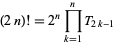 |
(2) |
(K. MacMillan, pers. comm., Jan. 21, 2008).
The factorial 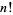 gives the number of ways in which
gives the number of ways in which 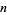 objects can be permuted. For example,
objects can be permuted. For example, 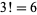 , since the six possible permutations of
, since the six possible permutations of {1,2,3}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline12.gif" style="height:15px; width:47px" /> are
{1,2,3}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline13.gif" style="height:15px; width:47px" />,
{1,3,2}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline14.gif" style="height:15px; width:47px" />,
{2,1,3}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline15.gif" style="height:15px; width:47px" />,
{2,3,1}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline16.gif" style="height:15px; width:47px" />,
{3,1,2}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline17.gif" style="height:15px; width:47px" />,
{3,2,1}" src="http://mathworld.wolfram.com/images/equations/Factorial/Inline18.gif" style="height:15px; width:47px" />. The first few factorials for
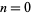 , 1, 2, ... are 1, 1, 2, 6, 24, 120, ... (OEIS A000142).
, 1, 2, ... are 1, 1, 2, 6, 24, 120, ... (OEIS A000142).
The numbers of digits in 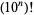 for
for 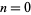 , 1, ... are 1, 7, 158, 2568, 35660, 456574, 5565709, 65657060, ... (OEIS A061010).
, 1, ... are 1, 7, 158, 2568, 35660, 456574, 5565709, 65657060, ... (OEIS A061010).
Generalizations of the factorial such as the double factorial 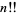 and multifactorial
and multifactorial 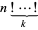 can be defined. Note, however, that these are not equal to nested factorials
can be defined. Note, however, that these are not equal to nested factorials 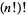 ,
, 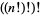 , etc.
, etc.
The first few values of 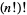 for
for 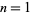 , 2, ... are 1, 2, 720, 620448401733239439360000, ... (Eureka 1974; OEIS A000197). The numbers of digits in
, 2, ... are 1, 2, 720, 620448401733239439360000, ... (Eureka 1974; OEIS A000197). The numbers of digits in 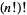 are 1, 1, 3, 24, 199, 1747, ... (OEIS A063979).
are 1, 1, 3, 24, 199, 1747, ... (OEIS A063979).
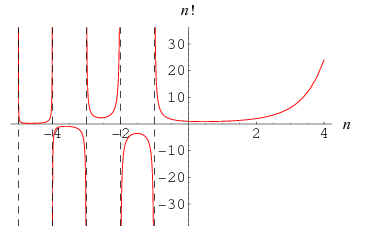
As 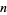 grows large, factorials begin acquiring tails of trailing zeros. To calculate the number
grows large, factorials begin acquiring tails of trailing zeros. To calculate the number 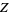 of trailing zeros for
of trailing zeros for 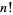 , use
, use
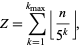 |
(3) |
where
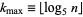 |
(4) |
and 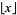 is the floor function (Gardner 1978, p. 63; Ogilvy and Anderson 1988, pp. 112-114). For
is the floor function (Gardner 1978, p. 63; Ogilvy and Anderson 1988, pp. 112-114). For 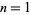 , 2, ..., the number of trailing zeros are 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, ... (OEIS A027868). This is a special application of the general result first discovered by Legendre in 1808 that the largest power of a prime
, 2, ..., the number of trailing zeros are 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, ... (OEIS A027868). This is a special application of the general result first discovered by Legendre in 1808 that the largest power of a prime 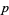 dividing
dividing 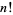 is
is
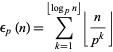 |
(5) |
(Landau 1974, pp. 75-76; Honsberger 1976; Hardy and Wright 1979, pp. 342; Ribenboim 1989; Ingham 1990, p. 20; Graham et al. 1994; Vardi 1991; Hardy 1999, pp. 18 and 21; Havil 2003, p. 165; Boros and Moll 2004, p. 5). This can be implemented in the Wolfram Language as
HighestPower[p_?PrimeQ, n_] :=
Sum[Floor[n/p^k], {k, Floor[Log[p,n]]}]
Stated another way, the exact power of a prime 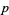 which divides
which divides 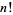 is
is
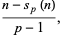 |
(6) |
where 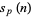 is the digit sum of
is the digit sum of 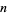 in base
in base 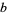 (Boros and Moll 2004, p. 6). This can be implemented in the Wolfram Language as
(Boros and Moll 2004, p. 6). This can be implemented in the Wolfram Language as
HighestPower2[p_Integer?PrimeQ, n_] :=
(n - Total[IntegerDigits[n, p]])/(p - 1)
Therefore, as shown by Legendre,
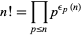 |
(7) |
(Havil 2003, p. 165).
Let 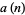 be the last nonzero digit in
be the last nonzero digit in 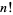 , then the first few values are 2, 6, 4, 2, 2, 4, 2, 8, 8, 8, 6, 8, ... (OEIS A008904). This sequence was studied by Kakutani (1967), who showed that this sequence is "5-automatic," meaning roughly that there exists a finite automaton which, when given the digits of
, then the first few values are 2, 6, 4, 2, 2, 4, 2, 8, 8, 8, 6, 8, ... (OEIS A008904). This sequence was studied by Kakutani (1967), who showed that this sequence is "5-automatic," meaning roughly that there exists a finite automaton which, when given the digits of 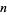 in base-5, will wind up in a state for which an output mapping specifies
in base-5, will wind up in a state for which an output mapping specifies  . The exact distribution of digits follows from this result.
. The exact distribution of digits follows from this result.
 |
By noting that
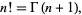 |
(8) |
where 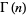 is the gamma function for integers
is the gamma function for integers 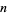 , the definition can be generalized to complex values
, the definition can be generalized to complex values
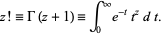 |
(9) |
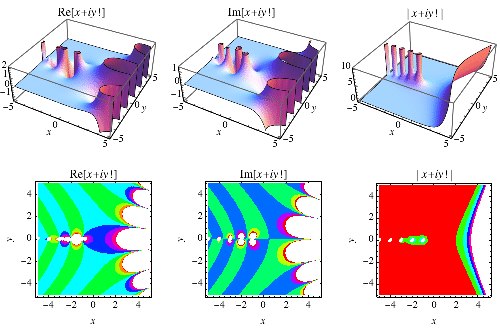
This defines 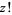 for all complex values of
for all complex values of 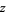 , except when
, except when 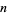 is a negative integer, in which case
is a negative integer, in which case 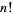 is equal to complex infinity.
is equal to complex infinity.
While Gauss (G1) introduced the notation
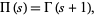 |
(10) |
this notation was subsequently abandoned after Legendre introduced the gamma-notation (Edwards 2001, p. 8).
Using the identities for gamma functions, the values of 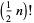 (half integral values) can be written explicitly
(half integral values) can be written explicitly
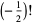 |
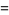 |
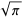 |
(11) |
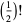 |
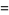 |
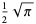 |
(12) |
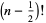 |
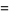 |
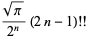 |
(13) |
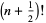 |
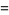 |
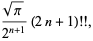 |
(14) |
where 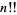 is a double factorial.
is a double factorial.
For integers 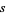 and
and 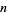 with
with 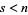 ,
,
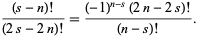 |
(15) |
The logarithm of 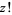 is frequently encountered
is frequently encountered
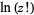 |
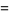 |
![1/2ln[(piz)/(sin(piz))]-gammaz-sum_(n=1)^(infty)(zeta(2n+1))/(2n+1)z^(2n+1)](http://mathworld.wolfram.com/images/equations/Factorial/Inline71.gif) |
(16) |
 |
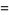 |
![1/2ln[(piz)/(sin(piz))]-1/2ln((1+z)/(1-z))+(1-gamma)z-sum_(n=1)^(infty)[zeta(2n+1)-1](z^(2n+1))/(2n+1)](http://mathworld.wolfram.com/images/equations/Factorial/Inline74.gif) |
(17) |
 |
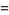 |
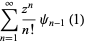 |
(18) |
 |
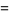 |
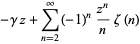 |
(19) |
 |
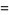 |
/n,](http://mathworld.wolfram.com/images/equations/Factorial/Inline83.gif) |
(20) |
where 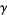 is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 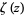 is the Riemann zeta function, and
is the Riemann zeta function, and 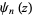 is the polygamma function.
is the polygamma function.
It is also given by the limit
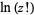 |
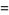 |
![ln[lim_(n->infty)(zn!)/((z)_(n+1))n^z]](http://mathworld.wolfram.com/images/equations/Factorial/Inline89.gif) |
(21) |
 |
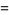 |
![ln[lim_(n->infty)(n!)/((z+1)_n)n^z]](http://mathworld.wolfram.com/images/equations/Factorial/Inline92.gif) |
(22) |
 |
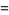 |
![ln[lim_(n->infty)(n!)/((z+1)(z+2)...(z+n))n^z]](http://mathworld.wolfram.com/images/equations/Factorial/Inline95.gif) |
(23) |
 |
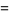 |
![lim_(n->infty)[ln(n!)+zlnn-ln(z+1)-ln(z+2)-...-ln(z+n)],](http://mathworld.wolfram.com/images/equations/Factorial/Inline98.gif) |
(24) |
where 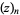 is the Pochhammer symbol.
is the Pochhammer symbol.
where 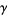 is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 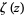 is the Riemann zeta function, and
is the Riemann zeta function, and 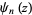 is the polygamma function. The factorial can be expanded in a series
is the polygamma function. The factorial can be expanded in a series
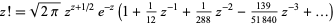 |
(25) |
(OEIS A001163 and A001164). Stirling's series gives the series expansion for 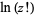 ,
,
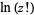 |
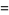 |
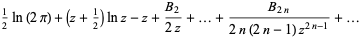 |
(26) |
 |
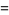 |
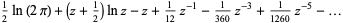 |
(27) |
(OEIS A046968 and A046969), where 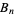 is a Bernoulli number.
is a Bernoulli number.
In general, the power-product sequences (Mudge 1997) are given by 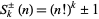 . The first few terms of
. The first few terms of 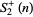 are 2, 5, 37, 577, 14401, 518401, ... (OEIS A020549), and
are 2, 5, 37, 577, 14401, 518401, ... (OEIS A020549), and 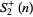 is prime for
is prime for 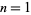 , 2, 3, 4, 5, 9, 10, 11, 13, 24, 65, 76, ... (OEIS A046029). The first few terms of
, 2, 3, 4, 5, 9, 10, 11, 13, 24, 65, 76, ... (OEIS A046029). The first few terms of 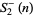 are 0, 3, 35, 575, 14399, 518399, ... (OEIS A046032), but
are 0, 3, 35, 575, 14399, 518399, ... (OEIS A046032), but 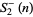 is prime for only
is prime for only 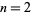 since
since 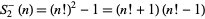 for
for 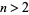 . The first few terms of
. The first few terms of 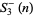 are 0, 7, 215, 13823, 1727999, ... (OEIS A046033), and the first few terms of
are 0, 7, 215, 13823, 1727999, ... (OEIS A046033), and the first few terms of 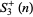 are 2, 9, 217, 13825, 1728001, ... (OEIS A019514).
are 2, 9, 217, 13825, 1728001, ... (OEIS A019514).
The first few numbers 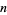 such that the sum of the factorials of their digits is equal to the prime counting function
such that the sum of the factorials of their digits is equal to the prime counting function 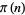 are 6500, 6501, 6510, 6511, 6521, 12066, 50372, ... (OEIS A049529). This sequence is finite, with the largest term being
are 6500, 6501, 6510, 6511, 6521, 12066, 50372, ... (OEIS A049529). This sequence is finite, with the largest term being 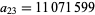 .
.
Numbers 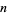 such that
such that
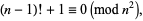 |
(28) |
are called Wilson primes.
Brown numbers are pairs 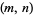 of integers satisfying the condition of Brocard's problem, i.e., such that
of integers satisfying the condition of Brocard's problem, i.e., such that
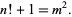 |
(29) |
Only three such pairs are known: (5, 4), (11, 5), (71, 7). Erdős conjectured that these are the only three such pairs (Guy 1994, p. 193).
REFERENCES:
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Caldwell, C. K. "The Top Twenty: Primorial and Factorial Primes." http://www.utm.edu/research/primes/lists/top20/PrimorialFactorial.html.
Conway, J. H. and Guy, R. K. "Factorial Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 65-66, 1996.
Dudeney, H. E. Amusements in Mathematics. New York: Dover, p. 96, 1970.
Edwards, H. M. "The Factorial Function." §in 1.3 Riemann's Zeta Function. New York: Dover, pp. 7-9, 2001.
Gardner, M. "Factorial Oddities." Ch. 4 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 50-65, 1978.
Gauss, C. F. "Disquisitiones Generales Circa Seriem Infinitam ![[(alphabeta)/(1·gamma)]x+[(alpha(alpha+1)beta(beta+1))/(1·2·gamma(gamma+1))]x^2](http://mathworld.wolfram.com/images/equations/Factorial/Inline127.gif)
![+[(alpha(alpha+1)(alpha+2)beta(beta+1)(beta+2))/(1·2·3·gamma(gamma+1)(gamma+2))]x^3+](http://mathworld.wolfram.com/images/equations/Factorial/Inline128.gif) etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.
etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.
Glynn, J. and Gray, T. The Beginner's Guide To Mathematica, Version 4. Cambridge, England: Cambridge University Press, 2000.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Factorial Factors." §4.4 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 111-115, 1994.
Guy, R. K. "Equal Products of Factorials," "Alternating Sums of Factorials," and "Equations Involving Factorial 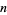 ." §B23, B43, and D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, and 193-194, 1994.
." §B23, B43, and D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, and 193-194, 1994.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Hoey, D. "Re: 01 squares." math-fun@cs.arizona.edu posting, May 19, 1997.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 2, 1976.
Ingham, A. E. The Distribution of Prime Numbers. Cambridge, England: Cambridge University Press, 1990.
Jeffreys, H. and Jeffreys, B. S. Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 462-463, 1988.
Kakutani, S. "Ergodic Theory of Shift Transformations." In Proc. 5th Berkeley Symposium on Mathematical Statistics and Probability, Vol. 2. Berkeley, CA: University of California Press, pp. 405-414, 1967.
Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, 1974.
Lewin, L. Dilogarithms and Associated Functions. London: Macdonald, 1958.
Leyland, P. http://www.leyland.vispa.com/numth/factorization/factors/factorial+.txt.
Leyland, P. http://www.leyland.vispa.com/numth/factorization/factors/factorial-.txt.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 174, 1979.
Mellin, H. "Abrißeiner einheitlichen Theorie der Gamma- und der hypergeometrischen Funktionen." Math. Ann. 68, 305-337, 1909.
Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.
Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, 1988.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, p. 86, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients." §6.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209, 1992.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 22-24, 1989.
Sloane, N. J. A. Sequences A000142/M1675, A000197/M2187, A001163/M5400, A001164/M4878, A008904, A019514, A020549, A027868, A046029, A046032, A046033, A046968, A046969, A049529, A061010, and A063979 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Factorial Function 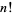 and Its Reciprocal." Ch. 2 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.
and Its Reciprocal." Ch. 2 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 19-33, 1987.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 81, 2004. http://www.mathematicaguidebooks.org/.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 67, 1991.
Vout, C. and Brown, M. "Problems Drive." Eureka 37, 11, 1974.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















