

علم الكيمياء

تاريخ الكيمياء والعلماء المشاهير

التحاضير والتجارب الكيميائية

المخاطر والوقاية في الكيمياء

اخرى

مقالات متنوعة في علم الكيمياء

كيمياء عامة


الكيمياء التحليلية

مواضيع عامة في الكيمياء التحليلية

التحليل النوعي والكمي

التحليل الآلي (الطيفي)

طرق الفصل والتنقية


الكيمياء الحياتية

مواضيع عامة في الكيمياء الحياتية

الكاربوهيدرات

الاحماض الامينية والبروتينات

الانزيمات

الدهون

الاحماض النووية

الفيتامينات والمرافقات الانزيمية

الهرمونات


الكيمياء العضوية

مواضيع عامة في الكيمياء العضوية

الهايدروكاربونات

المركبات الوسطية وميكانيكيات التفاعلات العضوية

التشخيص العضوي

تجارب وتفاعلات في الكيمياء العضوية


الكيمياء الفيزيائية

مواضيع عامة في الكيمياء الفيزيائية

الكيمياء الحرارية

حركية التفاعلات الكيميائية

الكيمياء الكهربائية


الكيمياء اللاعضوية

مواضيع عامة في الكيمياء اللاعضوية

الجدول الدوري وخواص العناصر

نظريات التآصر الكيميائي

كيمياء العناصر الانتقالية ومركباتها المعقدة


مواضيع اخرى في الكيمياء

كيمياء النانو

الكيمياء السريرية

الكيمياء الطبية والدوائية

كيمياء الاغذية والنواتج الطبيعية

الكيمياء الجنائية


الكيمياء الصناعية

البترو كيمياويات

الكيمياء الخضراء

كيمياء البيئة

كيمياء البوليمرات

مواضيع عامة في الكيمياء الصناعية

الكيمياء الاشعاعية والنووية
The Unit Cell
المؤلف:
........
المصدر:
LibreTexts Project
الجزء والصفحة:
............
24-4-2019
2407
The Unit Cell
There are seven fundamentally different kinds of unit cells, which differ in the relative lengths of the edges and the angles between them (Figure 1.1). Each unit cell has six sides, and each side is a parallelogram. We focus primarily on the cubic unit cells, in which all sides have the same length and all angles are 90°, but the concepts that we introduce also apply to substances whose unit cells are not cubic.
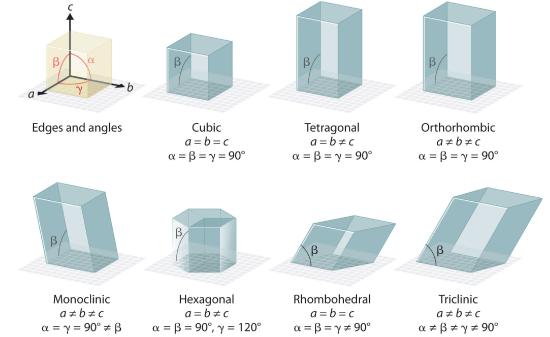
Figure 1.1 The General Features of the Seven Basic Unit Cells The lengths of the edges of the unit cells are indicated by a, b, and c, and the angles are defined as follows: α, the angle between b and c; β, the angle between a and c; and γ, the angle between a and b.
If the cubic unit cell consists of eight component atoms, molecules, or ions located at the corners of the cube, then it is called simple cubicA cubic unit cell that consists of eight component atoms, molecules, or ions located at the corners of a cube. (part (a) in Figure 1.2). If the unit cell also contains an identical component in the center of the cube, then it is body-centered cubic (bcc)A cubic unit cell with eight component atoms, molecules, or ions located at the corners of a cube plus an identical component in the center of the cube. (part (b) in Figure 1.2). If there are components in the center of each face in addition to those at the corners of the cube, then the unit cell is face-centered cubic (fcc)A cubic unit cell with eight component atoms, molecules, or ions located at the corners of a cube plus an identical component in the center of each face of the cube. (part (c) in Figure 1.2).

Figure 1.2 The Three Kinds of Cubic Unit Cell For the three kinds of cubic unit cells, simple cubic (a), body-centered cubic (b), and face-centered cubic (c), there are three representations for each: a ball-and-stick model, a space-filling cutaway model that shows the portion of each atom that lies within the unit cell, and an aggregate of several unit cells.
As indicated in Figure 1.2, a solid consists of a large number of unit cells arrayed in three dimensions. Any intensive property of the bulk material, such as its density, must therefore also be related to its unit cell. Because density is the mass of substance per unit volume, we can calculate the density of the bulk material from the density of a single unit cell. To do this, we need to know the size of the unit cell (to obtain its volume), the molar mass of its components, and the number of components per unit cell. When we count atoms or ions in a unit cell, however, those lying on a face, an edge, or a corner contribute to more than one unit cell, as shown in Figure 1.2. For example, an atom that lies on a face of a unit cell is shared by two adjacent unit cells and is therefore counted as 1/2 atom per unit cell. Similarly, an atom that lies on the edge of a unit cell is shared by four adjacent unit cells, so it contributes 1/4 atom to each. An atom at a corner of a unit cell is shared by all eight adjacent unit cells and therefore contributes 1/8 atom to each.The statement that atoms lying on an edge or a corner of a unit cell count as 1/4 or 1/8 atom per unit cell, respectively, is true for all unit cells except the hexagonal one, in which three unit cells share each vertical edge and six share each corner (Figure 1.1), leading to values of 1/3 and 1/6 atom per unit cell, respectively, for atoms in these positions. In contrast, atoms that lie entirely within a unit cell, such as the atom in the center of a body-centered cubic unit cell, belong to only that one unit cell.
 الاكثر قراءة في مقالات متنوعة في علم الكيمياء
الاكثر قراءة في مقالات متنوعة في علم الكيمياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















