
Lommel Polynomial
 المؤلف:
Iyanaga, S. and Kawada, Y.
المؤلف:
Iyanaga, S. and Kawada, Y.
 المصدر:
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press
المصدر:
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-3-2019
25-3-2019
 1956
1956
Lommel Polynomial
The Lommel polynomials 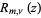 arise from the equation
arise from the equation
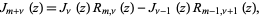 |
(1)
|
where 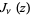 is a Bessel function of the first kind and
is a Bessel function of the first kind and  is a complex number (Watson 1966, p. 294). The function is given for
is a complex number (Watson 1966, p. 294). The function is given for 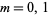 by
by
where 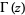 is a gamma function,
is a gamma function, 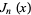 is a Bessel function of the first kind, and
is a Bessel function of the first kind, and 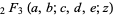 is a generalized hypergeometric function. Since (1) must reduce to the usual recurrence formula for Bessel functions, it follows that
is a generalized hypergeometric function. Since (1) must reduce to the usual recurrence formula for Bessel functions, it follows that
REFERENCES:
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, p. 294, 1966.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


