Residue Theorem
المؤلف:
Knopp, K.
المصدر:
"The Residue Theorem." §33 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover,
الجزء والصفحة:
...
18-12-2018
2007
Residue Theorem
An analytic function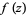 
whose Laurent series is given by
 |
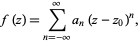(1)
|
can be integrated term by term using a closed contour 
encircling 
,
The Cauchy integral theorem requires that the first and last terms vanish, so we have
 |
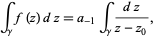(4)
|
where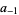 
is the complex residue. Using the contour 
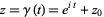gives
 |
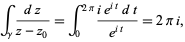(5)
|
so we have
 |
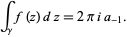(6)
|
If the contour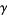 
encloses multiple poles, then the theorem gives the general result
 |
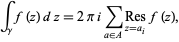(7)
|
where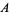 
is the set of poles contained inside the contour. This amazing theorem therefore says that the value of a contour integral for any contour in the complex plane depends only on the properties of a few very special points insidethe contour.
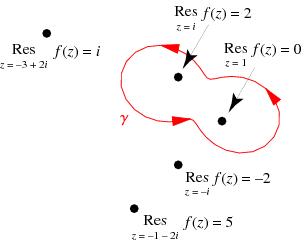
The diagram above shows an example of the residue theorem applied to the illustrated contour 
and the function
 |
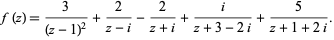(8)
|
Only the poles at 1 and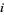 
are contained in the contour, which have residues of 0 and 2, respectively. The values of the contour integral is therefore given by
 |
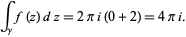(9)
|
REFERENCES:
Knopp, K. "The Residue Theorem." §33 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 129-134, 1996.
Krantz, S. G. "The Residue Theorem." §4.4.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 48-49, 1999.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
