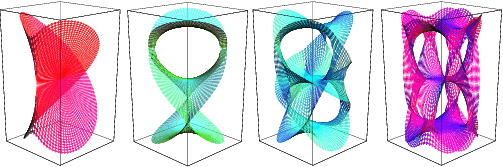
A Riemann surface is a surface-like configuration that covers the complex plane with several, and in general infinitely many, "sheets." These sheets can have very complicated structures and interconnections (Knopp 1996, pp. 98-99). Riemann surfaces are one way of representing multiple-valued functions; another is branch cuts. The above plot shows Riemann surfaces for solutions of the equation

with 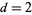, 3, 4, and 5, where  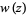is the Lambert W-function (M. Trott).

The Riemann surface 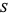 of the function field  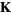is the set of nontrivial discrete valuations on 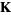. Here, the set  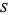corresponds to the ideals of the ring  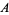of integers of  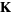over 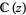. ( 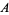consists of the elements of  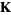that are roots of monic polynomials over .) Riemann surfaces provide a geometric visualization of functions elements and their analytic continuations.

Schwarz proved at the end of nineteenth century that the automorphism group of a compact Riemann surface of genus 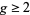 is finite, and Hurwitz (1893) subsequently showed that its order is at most  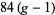(Arbarello et al. 1985, pp. 45-47; Karcher and Weber 1999, p. 9). This bound is attained for infinitely many 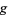, with the smallest  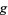of such an extremal surface being 3 (corresponding to the Klein quartic). However, it is also known that there are infinitely many genera for which the bound  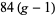is not attained (Belolipetsky 1997, Belolipetsky and Jones).

REFERENCES:

Arbarello, E.; Cornalba, M.; Griffiths, P. A.; and Harris, J. Geometry of Algebraic Curves, I. New York: Springer-Verlag, 1985.

Belolipetsky, M. "On the Number of Automorphisms of a Nonarithmetic Riemann Surface." Siberian Math. J. 38, 860-867, 1997.

Belolipetsky, M. and Jones, G. "A Bound for the Number of Automorphisms of an Arithmetic Riemann Surface." Math. Proc. Camb. Phil. Soc. 138, 289-299, 2005.

Borwein, J. M. and Corless, R. M. "Emerging Tools for Experimental Mathematics." Amer. Math. Monthly 106, 899-909, 1999.

Corless, R. M. and Jeffrey, D. J. "Graphing Elementary Riemann Surfaces." ACM Sigsam Bulletin: Commun. Comput. Algebra 32, 11-17, 1998.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 209-210, 2004.

Fischer, G. (Ed.). Plates 123-126 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, pp. 120-123, 1986.

Hurwitz, A. "Über algebraische Gebilde mit eindeutigen Transformationen in sich." Math. Ann. 41, 403-442, 1893.

Karcher, H. and Weber, M. "The Geometry of Klein's Riemann Surface." In The Eightfold Way: The Beauty of the Klein Quartic (Ed. S. Levy). New York: Cambridge University Press, pp. 9-49, 1999.

Knopp, K. Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 99-118, 1996.

Krantz, S. G. "The Idea of a Riemann Surface." §10.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 135-139, 1999.

Kulkarni, R. S. "Pseudofree Actions and Hurwitz's  Theorem." Math. Ann. 261, 209-226, 1982.

Lehner, J. and Newman, M. "On Riemann Surfaces with Maximal Automorphism Groups." Glasgow Math. J. 8, 102-112, 1967.

Macbeath, A. M. "On a Curve of Genus 7." Proc. Amer. Math. Soc. 15, 527-542, 1965.

Mathews, J. H. and Howell, R. W. Complex Analysis for Mathematics and Engineering, 4th ed. Boston, MA: Jones and Bartlett, 2000.

Monna, A. F. Dirichlet's Principle: A Mathematical Comedy of Errors and Its Influence on the Development of Analysis. Utrecht, Netherlands: Osothoek, Scheltema, and Holkema, 1975.

Springer, G. Introduction to Riemann Surfaces, 2nd ed. New York: Chelsea, 1981.

Trott, M. "Visualization of Riemann Surfaces of Algebraic Functions." Mathematica J. 6, 15-36, 1997.

Trott, M. "Visualization of Riemann Surfaces IIa." Mathematica J. 7, 465-496, 2000.

 Trott, M. "Visualization of Riemann Surfaces." http://library.wolfram.com/examples/riemannsurface/.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد