
Green,s Theorem
 المؤلف:
Kaplan, W
المؤلف:
Kaplan, W
 المصدر:
"Green,s Theorem." §5.5 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley
المصدر:
"Green,s Theorem." §5.5 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley
 الجزء والصفحة:
...
الجزء والصفحة:
...
 29-9-2018
29-9-2018
 2800
2800
Green's Theorem
Green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Over a region 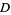 in the plane with boundary
in the plane with boundary 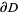 , Green's theorem states
, Green's theorem states
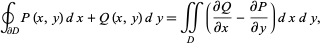 |
(1)
|
where the left side is a line integral and the right side is a surface integral. This can also be written compactly in vector form as
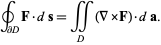 |
(2)
|
If the region 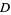 is on the left when traveling around
is on the left when traveling around 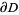 , then area of
, then area of 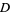 can be computed using the elegant formula
can be computed using the elegant formula
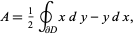 |
(3)
|
giving a surprising connection between the area of a region and the line integral around its boundary. For a plane curve specified parametrically as 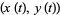 for
for ![t in [t_0,t_1]](http://mathworld.wolfram.com/images/equations/GreensTheorem/Inline7.gif) , equation (3) becomes
, equation (3) becomes
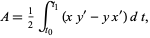 |
(4)
|
which gives the signed area enclosed by the curve.
The symmetric for above corresponds to Green's theorem with 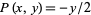 and
and 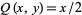 , leading to
, leading to
However, we are also free to choose other values of 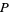 and
and 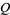 , including
, including 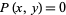 and
and 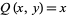 , giving the "simpler" form
, giving the "simpler" form
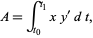 |
(10)
|
and 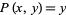 and
and 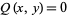 , giving
, giving
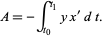 |
(11)
|
A similar procedure can be applied to compute the moment about the  -axis using
-axis using 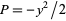 and
and 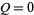 as
as
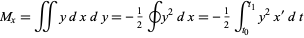 |
(12)
|
and about the 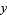 -axis using
-axis using 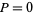 and
and 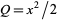 as
as
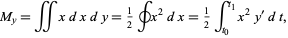 |
(13)
|
where the geometric centroid 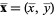 is given by
is given by 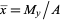 and
and 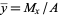 .
.
Finally, the area moments of inertia can be computed using 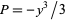 and
and 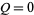 as
as
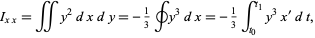 |
(14)
|
using 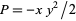 and
and 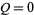 as
as
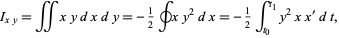 |
(15)
|
and using 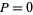 and
and 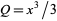 as
as
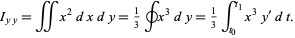 |
(16)
|
REFERENCES:
Arfken, G. "Gauss's Theorem." §1.11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 57-61, 1985.
Kaplan, W. "Green's Theorem." §5.5 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 286-291, 1991.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


