In general, there are two important types of curvature: extrinsic curvature and intrinsic curvature. The extrinsic curvature of curves in two- and three-space was the first type of curvature to be studied historically, culminating in the Frenet formulas, which describe a space curve entirely in terms of its "curvature," torsion, and the initial starting point and direction.

After the curvature of two- and three-dimensional curves was studied, attention turned to the curvature of surfaces in three-space. The main curvatures that emerged from this scrutiny are the mean curvature, Gaussian curvature, and the shape operator. Mean curvature was the most important for applications at the time and was the most studied, but Gauss was the first to recognize the importance of the Gaussian curvature.

Because Gaussian curvature is "intrinsic," it is detectable to two-dimensional "inhabitants" of the surface, whereas mean curvature and the shape operator are not detectable to someone who can't study the three-dimensional space surrounding the surface on which he resides. The importance of Gaussian curvature to an inhabitant is that it controls the surface area of spheres around the inhabitant.

Riemann and many others generalized the concept of curvature to sectional curvature, scalar curvature, the Riemann tensor, Ricci curvature tensor, and a host of other intrinsic and extrinsic curvatures. General curvatures no longer need to be numbers, and can take the form of a map, group, groupoid, tensor field, etc.

The simplest form of curvature and that usually first encountered in calculus is an extrinsic curvature. In two dimensions, let a plane curve be given by Cartesian parametric equations 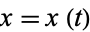 and 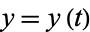. Then the curvature 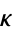, sometimes also called the "first curvature" (Kreyszig 1991, p. 47), is defined by

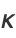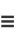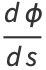			(1)
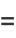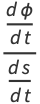			(2)
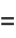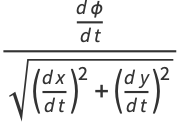			(3)
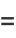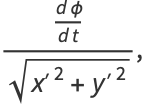			(4)

where 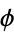 is the tangential angle and  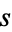is the arc length. As can readily be seen from the definition, curvature therefore has units of inverse distance. The  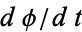derivative in the above equation can be found using the identity

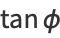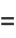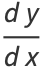			(5)
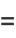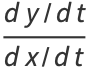			(6)
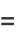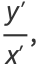			(7)

so

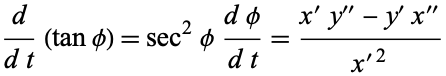(8)

and

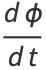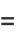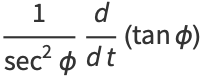			(9)
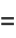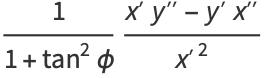			(10)
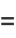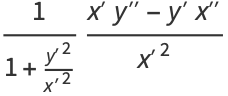			(11)
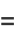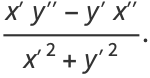			(12)

Combining equations (◇), 3), (10), and (12) then gives

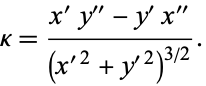(13)

For a two-dimensional curve written in the form 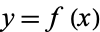, the equation of curvature becomes

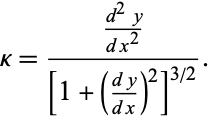(14)

If the two-dimensional curve is instead parameterized in polar coordinates, then

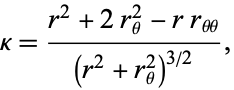(15)

where 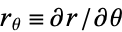 (Gray 1997, p. 89). In pedal coordinates, the curvature is given by

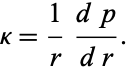(16)

The curvature for a two-dimensional curve given implicitly by 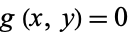 is given by

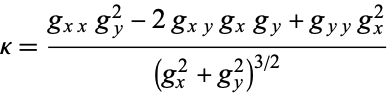(17)

(Gray 1997).

Now consider a parameterized space curve 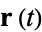 in three dimensions for which the tangent vector  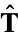is defined as

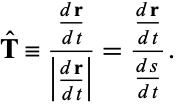(18)

Therefore,

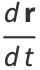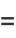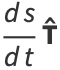			(19)
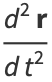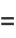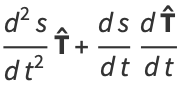			(20)
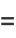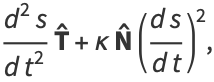			(21)

where 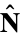 is the normal vector. But

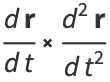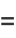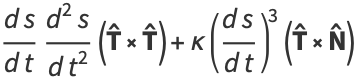			(22)
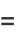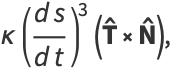			(23)

so taking norms of both sides gives

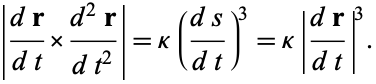(24)

Solving for 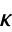 then gives

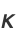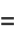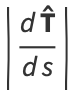			(25)
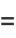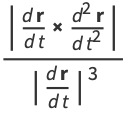			(26)
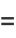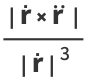			(27)

(Gray 1997, p. 192).

The curvature of a two-dimensional curve is related to the radius of curvature of the curve's osculating circle. Consider a circlespecified parametrically by

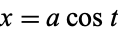(28)

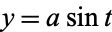(29)

which is tangent to the curve at a given point. The curvature is then

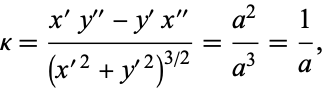(30)

or one over the radius of curvature. The curvature of a circle can also be repeated in vector notation. For the circle with 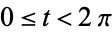, the arc length is

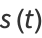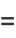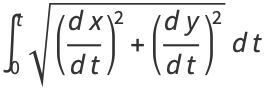			(31)
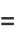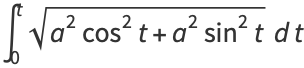			(32)
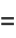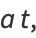			(33)

so 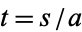 and the equations of the circle can be rewritten as

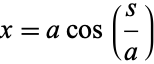(34)

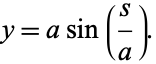(35)

The radius vector is then given by

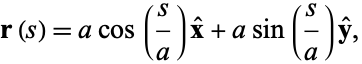(36)

and the tangent vector is

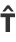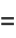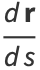			(37)
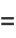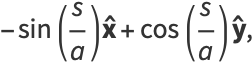			(38)

so the curvature is related to the radius of curvature 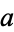 by

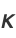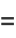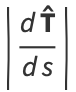			(39)
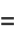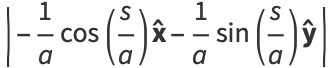			(40)
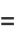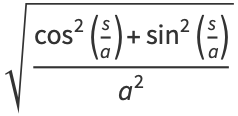			(41)
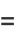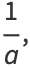			(42)

as expected.

Four very important derivative relations in differential geometry related to the Frenet formulas are

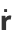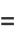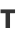			(43)
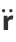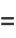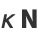			(44)
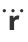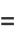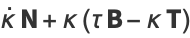			(45)
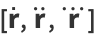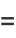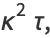			(46)

where 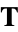 is the tangent vector,  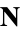is the normal vector,  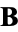is the binormal vector, and  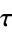is the torsion (Coxeter 1969, p. 322).

The curvature at a point on a surface takes on a variety of values as the plane through the normal varies. As 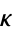 varies, it achieves a minimum and a maximum (which are in perpendicular directions) known as the principal curvatures. As shown in Coxeter (1969, pp. 352-353),

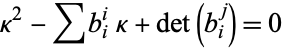(47)

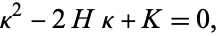(48)

where 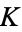 is the Gaussian curvature,  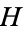is the mean curvature, and det denotes the determinant.

The curvature 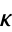 is sometimes called the first curvature and the torsion  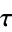the second curvature. In addition, a third curvature(sometimes called total curvature)

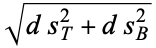(49)

is also defined. A signed version of the curvature of a circle appearing in the Descartes circle theorem for the radius of the fourth of four mutually tangent circles is called the bend.

REFERENCES:

Casey, J. Exploring Curvature. Wiesbaden, Germany: Vieweg, 1996.

Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.

Fischer, G. (Ed.). Plates 79-85 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, pp. 74-81, 1986.

Gray, A. "Curvature of Curves in the Plane," "Drawing Plane Curves with Assigned Curvature," and "Drawing Space Curves with Assigned Curvature." §1.5, 6.4, and 10.2 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 14-17, 140-146, and 222-224, 1997.

Kreyszig, E. "Principal Normal, Curvature, Osculating Circle." §12 in Differential Geometry. New York: Dover, pp. 34-36, 1991.

Yates, R. C. "Curvature." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 60-64, 1952.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد