
Reuleaux Tetrahedron
 المؤلف:
Encyclopedia Geometrica. "3D Reuleaux
المؤلف:
Encyclopedia Geometrica. "3D Reuleaux
 المصدر:
Encyclopedia Geometrica. "3D Reuleaux
المصدر:
Encyclopedia Geometrica. "3D Reuleaux
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-8-2018
25-8-2018
 2435
2435
Reuleaux Tetrahedron
The Reuleaux tetrahedron, sometimes also called the spherical tetrahedron, is the three-dimensional solid common to four spheres of equal radius placed so that the center of each sphere lies on the surface of the other three. The centers of the spheres are therefore located at the vertices of a regular tetrahedron, and the solid consists of an "inflated" tetrahedron with four curved edges.
Note that the name, coined here for the first time, is based on the fact that the geometric shape is the three-dimensional analog of the Reuleaux triangle, not the fact that it has constant width. In fact, the Reuleaux tetrahedron is not a solid of constant width. However, Meißner (1911) showed how to modify the Reuleaux tetrahedron to form a surface of constant width by replacing three of its edge arcs by curved patches formed as the surfaces of rotation of a circular arc. Depending on which three edge arcs are replaced (three that have a common vertex or three that form a triangle), one of two noncongruent shapes can be produced that are sometimes called Meissner tetrahedra (Lachand-Robert and Oudet 2007).
To analyze the Reuleaux tetrahedron, fix a tetrahedron of unit edge length with its vertices at the points 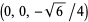 ,
, 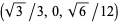 ,
, 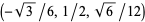 , and
, and 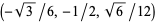 . Simultaneously solving the equations of three of four spheres for
. Simultaneously solving the equations of three of four spheres for  and
and 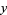 as a function of
as a function of 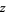 then gives
then gives
Half an arc is traced out as 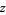 passes from
passes from 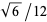 to
to 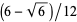 , and
, and
so the arc length of the curves connecting the vertices is given by
Making a change of coordinates,
Using the Gauss-Bonnet formula gives surface area as
(OEIS A202473; Harbourne).
The volume is significantly trickier to calculate analytically. Set up spherical coordinates from the centroid of the tetrahedron, so that the distance from the bottom vertex to the radius vector is 1, i.e.,
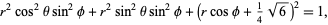 |
(12)
|
which simplifies to
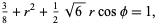 |
(13)
|
giving
![r(theta,phi)=1/4[sqrt(3cos(2phi)+13)-sqrt(6)cosphi].](http://mathworld.wolfram.com/images/equations/ReuleauxTetrahedron/NumberedEquation3.gif) |
(14)
|
By symmetry, the volume of the Reuleaux tetrahedron is given by
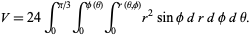 |
(15)
|
The integral over 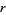 can be done immediately,
can be done immediately,
![V=1/8int_0^(pi/3)int_0^(phi(theta))[sqrt(3cos(2phi)+13)-sqrt(6)cosphi]^3sinphidphidtheta.](http://mathworld.wolfram.com/images/equations/ReuleauxTetrahedron/NumberedEquation5.gif) |
(16)
|
Now parameterize the top right edge as a function of the azimuthal coordinate 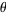 as
as
The polar angle 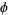 can then be solved for as a function of
can then be solved for as a function of 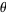 as
as
The integral over 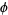 can be done by making the change of coordinates
can be done by making the change of coordinates
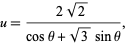 |
(22)
|
giving
![V=int_0^(pi/3)1/(32)[256-45sqrt(6)+42sqrt(6)cos(2tan^(-1)u)-(58sqrt(13+3cos(2tan^(-1)u)))/(sqrt(1+u^2))+6sqrt(13+3cos(2tan^(-1)u))cos(3tan^(-1)u)+3sqrt(6)cos(4tan^(-1)u)]dtheta.](http://mathworld.wolfram.com/images/equations/ReuleauxTetrahedron/NumberedEquation7.gif) |
(23)
|
Making the change of variables
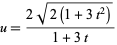 |
(24)
|
then gives the volume as
![V=int_0^1[(8sqrt(3))/(1+3t^2)-(16sqrt(2)(3t+1)(4t^2+t+1)^(3/2))/((3t^2+1)(11t^2+2t+3)^2)-(sqrt(2)(249t^2+54t+65))/((11t^2+2t+3)^2)]dt.](http://mathworld.wolfram.com/images/equations/ReuleauxTetrahedron/NumberedEquation9.gif) |
(25)
|
This integral can be done analytically using computer algebra, but the analytic form returned by symbolic algebra programs is a complicated expression involving logarithms and inverse tangent functions.
However, a much simpler approach using the surface area combined with some straightforward geometry gives the fully simplified form almost immediately as
(OEIS A102888; Harbourne).
REFERENCES:
Encyclopedia Geometrica. "3D Reuleaux." http://www.fastgeometry.com/Reuleaux/ConstantBreadth3DShapes.htm.
Harbourne, B. "Volume and Surface Area of the Spherical Tetrahedron (AKA Reuleaux Tetrahedron) by Geometrical Methods." http://www.math.unl.edu/~bharbourne1/ST/sphericaltetrahedron.html.
Lachand-Robert, T. and Oudet, É. "Bodies of Constant Width in Arbitrary Dimension." Math. Nachr. 280, 740-750, 2007.
Meissner, F. "Über Punktmengen konstanter Breite." Vierteljahresschr. naturforsch. Ges. Zürich 56, 42-50, 1911.
Sloane, N. J. A. Sequences A102888 and A202473 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


