Hypercube Point Picking
المؤلف:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E
المصدر:
"Box Integrals." Preprint. Apr. 3, 2006.
الجزء والصفحة:
...
20-8-2018
2242
Hypercube Point Picking
The expected value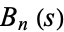 
of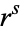 
from a fixed vertex of a unit 
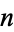-cube to a point picked at random in the interior of the hypercube is given by
where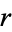 
is the distance and
(Bailey et al. 2006).
The first few values of expected distances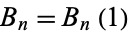 
are given by
where the term
is not known in closed form (Bailey et al. 2006; Bailey et al. 2007, pp. 238 and 272).
It is related to the expected distance from the center of the unit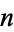 
-cube by
 |
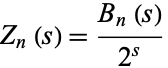(11)
|
(Bailey et al. 2006).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "Box Integrals." Preprint. Apr. 3, 2006.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action.Wellesley, MA: A K Peters, 2007.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
