

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Cosine
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
18-8-2018
3839
Cosine
 |
 |
The cosine function 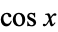 is one of the basic functions encountered in trigonometry (the others being the cosecant,cotangent, secant, sine, and tangent). Let
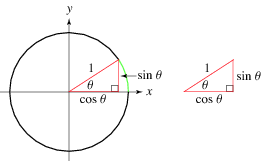
is one of the basic functions encountered in trigonometry (the others being the cosecant,cotangent, secant, sine, and tangent). Let 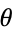 be an angle measured counterclockwise from the x-axis along the arc of the unit circle. Then
be an angle measured counterclockwise from the x-axis along the arc of the unit circle. Then  is the horizontal coordinate of the arc endpoint.
is the horizontal coordinate of the arc endpoint.
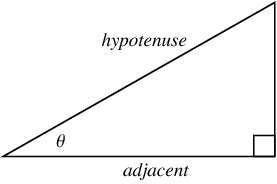
The common schoolbook definition of the cosine of an angle 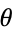 in a right triangle (which is equivalent to the definition just given) is as the ratio of the lengths of the side of the triangle adjacent to the angle and the hypotenuse, i.e.,
in a right triangle (which is equivalent to the definition just given) is as the ratio of the lengths of the side of the triangle adjacent to the angle and the hypotenuse, i.e.,
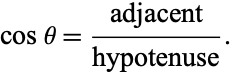 |
(1) |
A convenient mnemonic for remembering the definition of the sine, cosine, and tangent is SOHCAHTOA (sine equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, tangent equals opposite over adjacent).
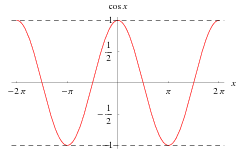
As a result of its definition, the cosine function is periodic with period 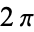 . By the Pythagorean theorem,
. By the Pythagorean theorem,  also obeys the identity
also obeys the identity
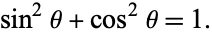 |
(2) |
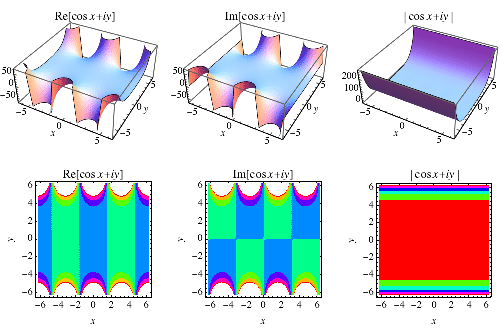 |
The definition of the cosine function can be extended to complex arguments 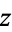 using the definition
using the definition
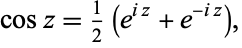 |
(3) |
where e is the base of the natural logarithm and i is the imaginary number. Cosine is an entire function and is implemented in the Wolfram Language as Cos[z].
A related function known as the hyperbolic cosine is similarly defined,
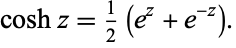 |
(4) |
The cosine function has a fixed point at 0.739085... (OEIS A003957), a value sometimes known as the Dottie number(Kaplan 2007).
The cosine function can be defined analytically using the infinite sum
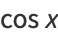 |
 |
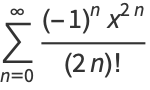 |
(5) |
 |
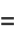 |
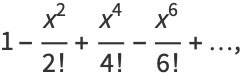 |
(6) |
or the infinite product
![cosx=product_(n=1)^infty[1-(4x^2)/(pi^2(2n-1)^2)].](http://mathworld.wolfram.com/images/equations/Cosine/NumberedEquation5.gif) |
(7) |

A close approximation to 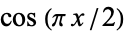 for
for ![x in [0,1]](http://mathworld.wolfram.com/images/equations/Cosine/Inline15.gif) is
is
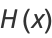 |
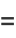 |
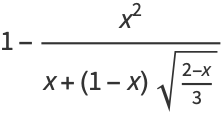 |
(8) |
 |
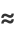 |
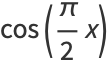 |
(9) |
(Hardy 1959), where the difference between 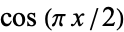 and Hardy's approximation is plotted above.
and Hardy's approximation is plotted above.
The cosine obeys the identity
![cos(ntheta)=2costhetacos[(n-1)theta]-cos[(n-2)theta]](http://mathworld.wolfram.com/images/equations/Cosine/NumberedEquation6.gif) |
(10) |
and the multiple-angle formula
![cos(nx)=sum_(k=0)^n(n; k)cos^kxsin^(n-k)xcos[1/2(n-k)pi],](http://mathworld.wolfram.com/images/equations/Cosine/NumberedEquation7.gif) |
(11) |
where 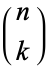 is a binomial coefficient. It is related to
is a binomial coefficient. It is related to 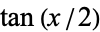 via
via
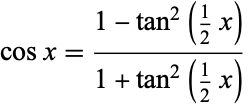 |
(12) |
(Trott 2006, p. 39).
Summation of 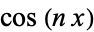 from
from 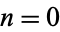 to
to 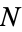 can be done in closed form as
can be done in closed form as
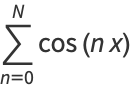 |
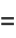 |
![R[sum_(n=0)^(N)e^(inx)]](http://mathworld.wolfram.com/images/equations/Cosine/Inline30.gif) |
(13) |
 |
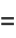 |
![R[(e^(i(N+1)x)-1)/(e^(ix)-1)]](http://mathworld.wolfram.com/images/equations/Cosine/Inline33.gif) |
(14) |
 |
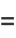 |
![R[(e^(i(N+1)x/2))/(e^(ix/2))(e^(i(N+1)x/2)-e^(-i(N+1)x/2))/(e^(ix/2)-e^(-ix/2))]](http://mathworld.wolfram.com/images/equations/Cosine/Inline36.gif) |
(15) |
 |
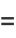 |
![(sin[1/2(N+1)x])/(sin(1/2x))R[e^(iNx/2)]](http://mathworld.wolfram.com/images/equations/Cosine/Inline39.gif) |
(16) |
 |
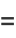 |
![(cos(1/2Nx)sin[1/2(N+1)x])/(sin(1/2x)).](http://mathworld.wolfram.com/images/equations/Cosine/Inline42.gif) |
(17) |
Similarly,
![sum_(n=0)^inftyp^ncos(nx)=R[sum_(n=0)^inftyp^ne^(inx)],](http://mathworld.wolfram.com/images/equations/Cosine/NumberedEquation9.gif) |
(18) |
where 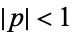 . The exponential sum formula gives
. The exponential sum formula gives
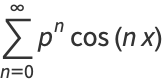 |
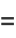 |
![R[(1-pe^(-ix))/(1-2pcosx+p^2)]](http://mathworld.wolfram.com/images/equations/Cosine/Inline46.gif) |
(19) |
 |
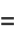 |
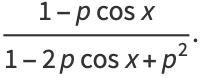 |
(20) |
The sum of 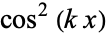 can also be done in closed form,
can also be done in closed form,
|
(21) |
The Fourier transform of 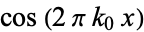 is given by
is given by
](http://mathworld.wolfram.com/images/equations/Cosine/Inline52.gif) |
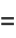 |
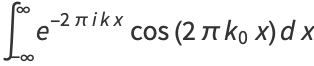 |
(22) |
 |
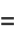 |
![1/2[delta(k-k_0)+delta(k+k_0)],](http://mathworld.wolfram.com/images/equations/Cosine/Inline57.gif) |
(23) |
where 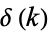 is the delta function.
is the delta function.
Cvijović and Klinowski (1995) note that the following series
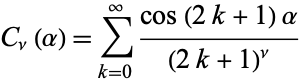 |
(24) |
has closed form for 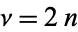 ,
,
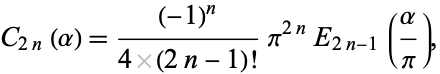 |
(25) |
where 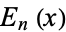 is an Euler polynomial.
is an Euler polynomial.
A definite integral involving 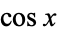 is given by
is given by
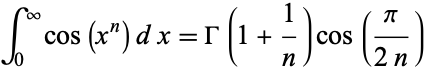 |
(26) |
for 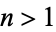 where
where 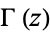 is the gamma function (T. Drane, pers. comm., Apr. 21, 2006).
is the gamma function (T. Drane, pers. comm., Apr. 21, 2006).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 215, 1987.
Cvijović, D. and Klinowski, J. "Closed-Form Summation of Some Trigonometric Series." Math. Comput. 64, 205-210, 1995.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 68, 1959.
Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.
Kaplan, S. R. "The Dottie Number." Math. Mag. 80, 73-74, 2007.
Project Mathematics. "Sines and Cosines, Parts I-III." Videotape. http://www.projectmathematics.com/sincos1.htm.
Sloane, N. J. A. Sequence A003957 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Sine 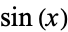 and Cosine
and Cosine 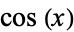 Functions." Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Functions." Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Tropfke, J. Teil IB, §1. "Die Begriffe des Sinus und Kosinus eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 11-23, 1923.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.
Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















