Adding Vectors by Components
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 41
12-12-2016
2608
Adding Vectors by Components
Finally we will now see the use of components and unit vectors. Remember how we discussed adding vectors graphically using a ruler and protractor. A better method is with the use of components, because then we can get our answers by pure calculation. In Fig. 1.1 we have shown two vectors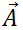 
and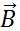 
added to form 
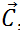, but we have also indicated all the components.
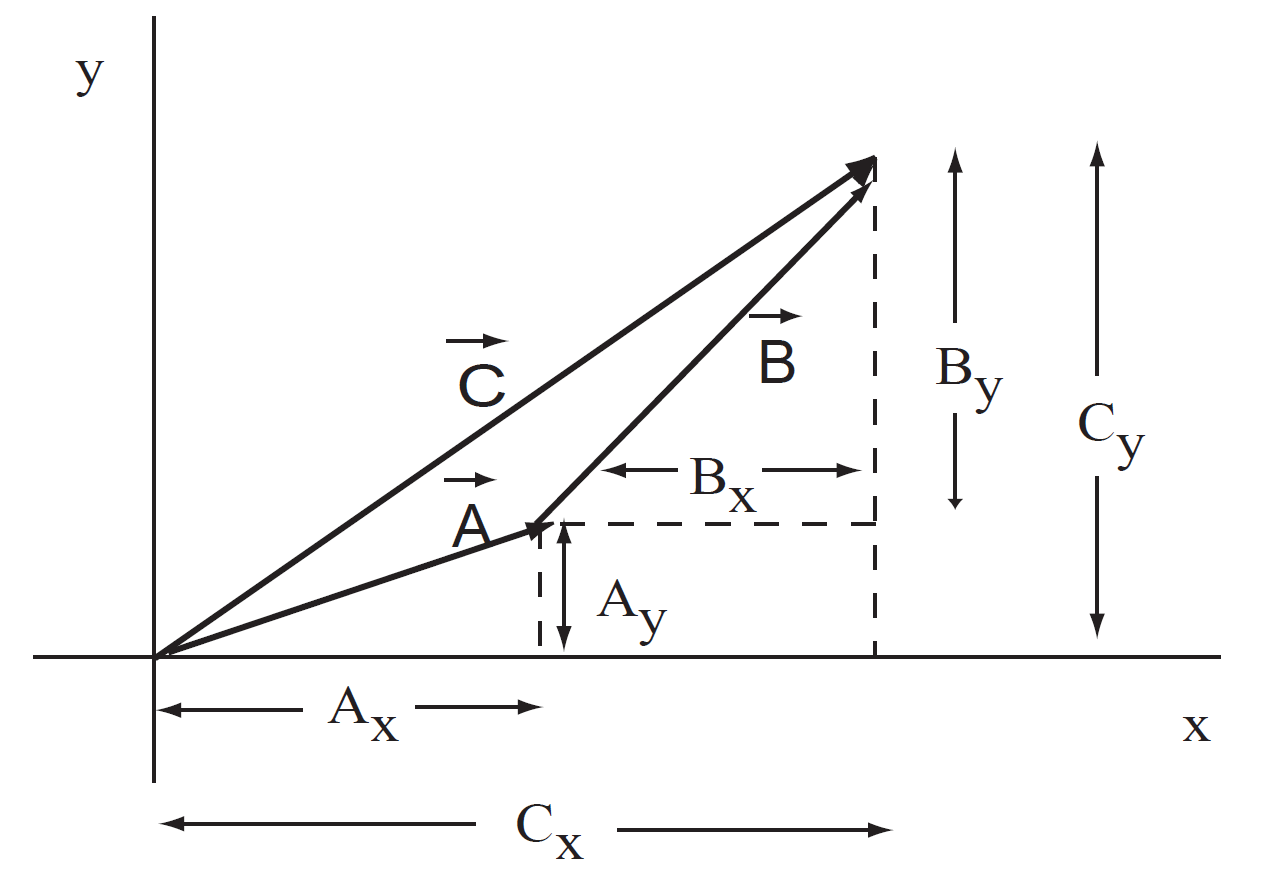
FIGURE 1.1 Adding vectors by components.
By carefully looking at the figure you can see that
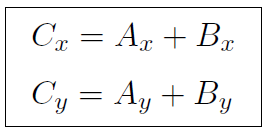
This is a very important result. Now let's back-track for a minute. When we write
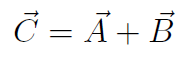
you should say, ''Wait a minute! What does the + sign mean?" We are used to adding numbers such as 5 = 3 + 2, but in the above equation , and 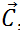are not numbers. They are these strange arrow-like objects called vectors which are ''add" by putting head-to-tail. We should really write
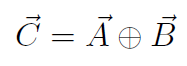
where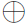 
is a new type of ''addition", totally unlike adding numbers. However Ax, Bx, Ay, By, Cx, Cy are ordinary numbers and the + sign we used above does denote ordinary addition. Thus 
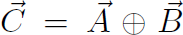actually means Cx = Ax + Bx and Cy = Ay + By. The statement 
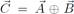is really shorthand for two ordinary addition statements. Whenever anyone writes something like 
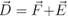it actually means two things, namely Dx = Fx+ Ex and Dy = Fy + Ey. All of this is much more obvious with the use of unit vectors. Write 
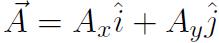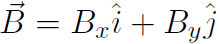and 
and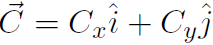 
. Now
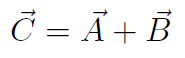
is simply
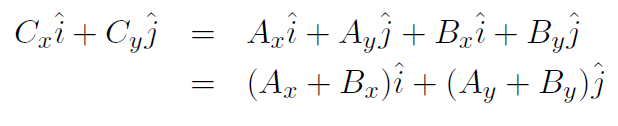
and equating coefficients of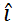 
and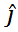 
gives
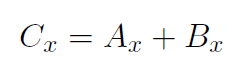
and
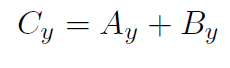
الاكثر قراءة في الفيزياء العامة
اخر الاخبار
اخبار العتبة العباسية المقدسة
