The Ancient Greeks had four great construction problems:

• trisecting the angle (dividing an angle into three equal smaller angles),

• doubling the cube (building a second cube with twice the volume of the first),

• squaring the circle (creating a square with the same area as a particular circle),

• constructing polygons (building regular shapes with equal sides and angles).

To perform these tasks they only used the bare essentials:

• a straight edge for drawing straight lines (and definitely not to measure lengths),

• a pair of compasses for drawing circles.

If you like climbing mountains without ropes, oxygen, mobile phones and other paraphernalia, these problems will undoubtedly appeal. Without modern measuring equipment the mathematical techniques needed to prove these results were sophisticated and the classical construction problems of antiquity were only solved in the 19th century using the techniques of modern analysis and abstract algebra.

Trisecting the angle

Here is a way to divide an angle into two equal smaller angles or, in other words, bisect it. First place the compass point at O and, with any radius mark off OA and OB. Moving the compass point to A, draw a portion of a circle. Do the same at B. Label the point of intersection of these circles P, and with the straight edge join O to P. The triangles AOP and BOP are identical in shape and therefore the angles AÔP and BÔP will be equal. The line OP is the required bisector, splitting the angle into two equal angles.

Can we use a sequence of actions like this to split an arbitrary angle into three equal angles? This is the angle trisection problem.

If the angle is 90 degrees, a right angle, there is no problem, because the angle of 30 degrees can be constructed. But, if we take the angle of 60 degrees, for instance this angle cannot be trisected. We know the answer is 20 degrees but there is no way of constructing this angle using only a straight edge and compasses. So summarizing:

• you can bisect all angles all the time,

• you can trisect some angles all the time, but

• you cannot trisect some angles at any time.

The duplication of the cube is a similar problem known as the Delian problem. The story goes that the natives of Delos in Greece consulted the oracle in the face of a plague they were suffering. They were told to construct a new altar, twice the volume of the existing one.

Imagine the Delian altar began as a three-dimensional cube with all sides equal in length, say a. So they needed to construct another cube of length b with twice its volume. The volume of each is a³ and b³ and they are related by b3 = 2a³ or b = ³√2 × a where ³√2 is the number multiplied by itself three times that makes 2 (the cube root). If the side of the original cube is a = 1 the natives of Delos had to mark off the length ³√2 on a line. Unfortunately for them, this is impossible with a straight edge and compasses no matter how much ingenuity is brought to bear on the would-be construction.

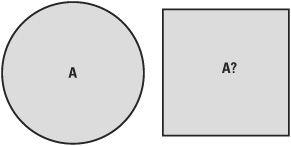
Squaring the circle

Squaring the circle

This problem is a little different and is the most famous of the construction problems:

To construct a square whose area is equal to the area of a given circle.

The phrase ‘squaring the circle’ is commonly used to express the impossible. The algebraic equation x² – 2 = 0 has specific solutions 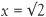and 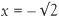. These are irrational numbers (they cannot be written as fractions), but showing the circle cannot be squared amounts to showing that π cannot be a solution of any algebraic equation. Irrational numbers with this property are called transcendental numbers because they have a ‘higher’ irrationality than their irrational cousins like √2.

Mathematicians generally believed that π was a transcendental but this ‘riddle of the ages’was difficult to prove until Ferdinand von Lindemann used a modification of a technique pioneered by Charles Hermite. Hermite had used it to deal with the lesser problem of proving that the base of natural logarithms, e, was transcendental .

Following Lindemann’s result, we might think that the flow of papers from the indomitable band of ‘circle-squarers’ would cease. Not a bit of it. Still dancing on the sidelines of mathematics were those reluctant to accept the logic of the proof and some who had never heard of it.

Constructing polygons

Euclid posed the problem of how to construct a regular polygon. This is a symmetrical many-sided figure like a square or pentagon, in which sides are all of equal length and where adjacent sides make equal angles with each other. In his famous work the Elements (Book 4), Euclid showed how the polygons with 3, 4, 5 and 6 sides could be constructed using only our two basic tools.

Constructing an equilateral triangle

The polygon with 3 sides is what we normally call an equilateral triangle and is particularly straightforward to construct. However long you want your triangle to be, label one point A and another B with the desired distance in between. Place the compass point at A and draw a portion of the circle of radius AB. Repeat this with the compass point at B using the same radius. The intersection point of these two arcs is at P. As AP = AB and BP = AB all three sides of the triangle APB are equal. The actual triangle is completed by joining AB, AP and BP using the straight edge.

If you think having a straight edge seems rather a luxury, you’re not alone – the Dane Georg Mohr thought so too. The equilateral triangle is constructed by finding the point P and for this only the compasses are required – the straight edge was only used to physically join the points together. Mohr showed that any construction achievable by straight edge and compasses can be achieved with the compasses alone. The Italian Lorenzo Mascheroni proved the same results 125 years later. A novel feature of his 1797 book Geometria del Compasso, dedicated to Napoleon, is that he wrote it in verse.

A prince is born

Carl Friedrich Gauss was so impressed by his result showing a 17-sided polygon could be constructed that he decided to put away his planned study of languages and become a mathematician. The rest is history – and he became known as the ‘prince of mathematicians’. The 17-sided polygon is the shape of the base of his memorial at Göttingen, Germany, and is a fitting tribute to his genius.

For the general problem, the polygons with p sides where p is a prime number are especially important. We have already constructed the 3-sided polygon, and Euclid constructed the 5-sided polygon but he could not construct the 7-sided polygon (the heptagon). Investigating this problem as a 17 year old, a certain Carl Friederich Gauss proved a negative. He deduced that it is not possible to construct a p-sided polygon for p = 7, 11 or 13.

But Gauss also proved a positive, and he concluded that it is possible to construct a 17-sided polygon. Gauss actually went further and proved that a p-sided polygon is constructable if and only if the prime number p is of the form

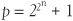
Numbers of this form are called Fermat numbers. If we evaluate them for n = 0, 1, 2, 3 and 4, we find they are the prime numbers p = 3, 5, 17, 257 and 65,537, and these correspond to a constructible polygon with p sides.

When we try n = 5, the Fermat number is p = 2³² + 1 = 4,294,967,297. Pierre de Fermat conjectured that they were all prime numbers, but unfortunately this one is not a prime number, because 4,294,967,297 = 641 × 6,700,417. If we put n = 6 or 7 into the formula the results are huge Fermat numbers but, as with 5, neither is prime.

Are there any other Fermat primes? The accepted wisdom is that there are not, but no one knows for sure.

the condensed idea

Take a straight edge and a pair of compasses . . .

مواضيع ذات صلة

π

Zero

Triangles

Topology

The travelling salesperson

The Riemann hypothesis

The parallel postulate

The normal curve

The four-colour problem

The diet problem

The birthday problem

Squares and square roots