سرعة الصوت

 ان سرعة الموجات المستعرضة على وتر مشدود تعطي بالعلاقة:

(1)          

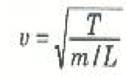
وهذه حالة خاصة من الصورة العامة الآتية:

وبناء على هذا يتوقع ان تتبع سرعة الموجات الطولية في أي وسط علاقة مشابهة. وهذا صحيح بالفعل، فقوة الاستعادة في حالة التضاغطات والتخلخلات مرتبطة بمعامل مرونة الوسط، كما ان عامل القصور الذاتي هو كثافة الوسط. وفي حالة الوسط أحادي البعد، كالسلك او قضيب السكة الحديد، يكون معامل المرونة المناسب هو معامل يونج Y، اما في حالة الأوساط ثنائية وثلاثية الأبعاد فيجب استخدام معامل المرونة الحجمية B. وعليه يمكننا كتابة التعبيرين الآتيين لسرعة الصوت:

(2)         

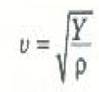
(وللوسط أحادي البعد)، و:

(3)           

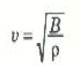
(للأوساط ثنائية وثلاثية الأبعاد).

لنطبق الآن المعادلة (3) على حالة سرعة الصوت في الغازات.

في حالة الغازات المثالية تعتمد قيمة B على نوع العملية التي ينضغط بها الغاز فإذا كان الانضغاط أيسوثرمياً فإن معامل المرونة الحجمية B يساوي الغاز P. ولكن التضاغطات الناتجة عن مرور الموجة الصوتية خلال حجم صغير من الغاز تحدث بطريقة فجائية سريعة جداً بحيث لا تكون هناك فرصة لحدوث أي تبادل حراري. وعليه فإن هذه التضاغطات تكون أدياباتية. وباستعمال قانون الغاز المثالي يمكننا بقليل من العمليات الرياضية البسيطة إثبات أن B = γP في حالة التضاغطات الأدياباتية، حيث γ =C_p / C_v .

إذن، تعطى سرعة الصوت في الغاز المثالي بالعلاقة:

(4)       

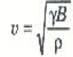
ولكن قانون الغاز المثالي يعطي ضغط الغاز بدلالة درجة حرارته كالتالي:

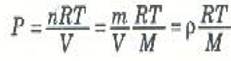
حيث m كتلة n moles من الغاز، M الكتلة الذرية او الجزيئية للغاز. إذن، بالتعويض عن P من هذه العلاقة في المعادلة (4) نجد ان:

(5)          

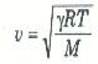
ومن المهم ملاحظة ان اعتماد سرعة الموجة الصوتية على كل من P و p طبقاً للمعادلة (4) قد اختفى هنا، إذ تبين المعادلة (5) أن درجة حرارة الغاز هي متغير الحالة الديناميكية الحرارية الذي تتعين به سرعة الصوت.

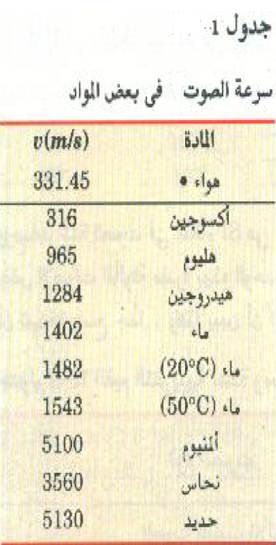
ويوضح الجدول ((1 القيم النموذجية لسرعة الصوت في بعض المواد عند 0^oC لاحظ ما ذكر في حاشية هذا الجدول عن تغير v في الهواء مع .T

مواضيع ذات صلة

Nonlinear responses

The energy theorem

Quality and consonance

The Fourier series

Musical tones

The speed of sound

The propagation of sound

Resonance in nature

Electrical resonance

الرنين الخطر

موسيقى الرياح

عجائب الصدى