The general expression for work
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص33-34
2025-11-01
61
The general expression for work
The calculation of expansion work starts from the definition used in physics, which states that the work required to move an object a distance dz against an opposing force of magnitude F is , dw= −Fdz , The negative sign tells us that, when the system moves an object against an opposing force, the internal energy of the system doing the work will decrease. Now consider the arrangement shown in Fig. 2.6, in which one wall of a system is a massless, frictionless, rigid, perfectly fitting piston of area A. If the external pressure is pex, the magnitude of the force acting on the outer face of the piston is F = pexA. When the system expands through a distance dz against an external pressure pex, it follows that the work done is dw =−pexAdz. But Adz is the change in volume, dV, in the course of the expansion. Therefore, the work done when the system expands by dV against a pressure pex is , dw=−pexdV , To obtain the total work done when the volume changes from Vi to Vf we integrate this expression between the initial and final volumes:
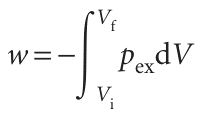
The force acting on the piston, pexA, is equivalent to a weight that is raised as the system expands. If the system is compressed instead, then the same weight is lowered in the surroundings and eqn 2.6 can still be used, but now Vf < Vi. It is important to note that it is still the external pressure that determines the magnitude of the work. This somewhat perplexing conclusion seems to be inconsistent with the fact that the gas inside the container is opposing the compression. However, when a gas is compressed, the ability of the surroundings to do work is diminished by an amount determined by the weight that is lowered, and it is this energy that is transferred into the system. Other types of work (for example, electrical work), which we shall call either non expansion work or additional work, have analogous expressions, with each one the product of an intensive factor (the pressure, for instance) and an extensive factor (the change in volume). Some are collected in Table 2.1. For the present we continue with the work associated with changing the volume, the expansion work, and see what we can extract from eqns 2.5 and 2.6.
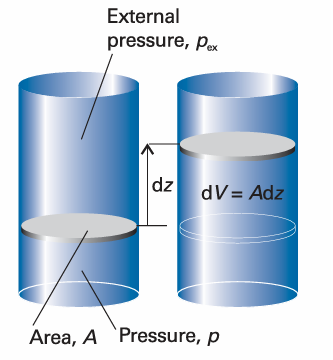
Fig. 2.6 When a piston of area A moves out through a distance dz, it sweeps out a volume dV = Adz. The external pressure pex is equivalent to a weight pressing on the piston, and the force opposing expansion is F=pexA.
الاكثر قراءة في مواضيع عامة في الكيمياء العضوية
اخر الاخبار
اخبار العتبة العباسية المقدسة
