Virial coefficients
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص15-16
2025-10-30
32
Virial coefficients
Figure 1.15 shows the experimental isotherms for carbon dioxide. At large molar volumes and high temperatures the real-gas isotherms do not differ greatly from perfect-gas isotherms. The small differences suggest that the perfect gas law is in fact the first term in an expression of the form , pVm=RT (1 + B′p +C′p2+ ···) (1.18)
This expression is an example of a common procedure in physical chemistry, in which a simple law that is known to be a good first approximation (in this case pV = nRT) is
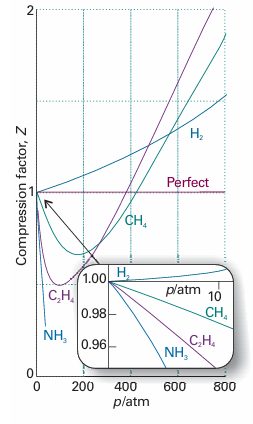
Fig. 1.14 The variation of the compression factor, Z, with pressure for several gases at 0°C. A perfect gas has Z = 1 at all pressures. Notice that, although the curves approach 1 as p → 0, they do so with different slopes.
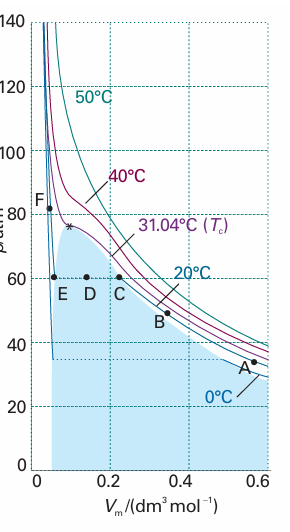
Fig. 1.15 Experimental isotherms of carbon dioxide at several temperatures. The ‘critical isotherm’, the isotherm at the critical temperature, is at 31.04°C. The critical point is marked with a star. treated as the first term in a series in powers of a variable (in this case p). A more convenient expansion for many applications is
These two expressions are two versions of the virial equation of state.4 By comparing the expression with eqn 1.17 we see that the term in parentheses can be identified with the compression factor, Z.
The coefficients B, C,..., which depend on the temperature, are the second, third, ...virial coefficients (Table 1.4); the first virial coefficient is 1. The third virial coefficient, C, is usually less important than the second coefficient, B, in the sense that at typical molar volumes C/V2m << B/Vm.
We can use the virial equation to demonstrate the important point that, although the equation of state of a real gas may coincide with the perfect gas law as p → 0, not all its properties necessarily coincide with those of a perfect gas in that limit. Consider, for example, the value of dZ/dp, the slope of the graph of compression factor against pressure. For a perfect gas dZ/dp = 0 (because Z = 1 at all pressures), but for a real gas from eqn 1.18 we obtain
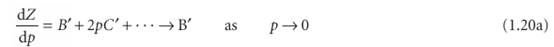
However, B′ is not necessarily zero, so the slope of Z with respect to p does not necessarily approach 0 (the perfect gas value), as we can see in Fig. 1.14. Because several physical properties of gases depend on derivatives, the properties of real gases do not always coincide with the perfect gas values at low pressures. By a similar argument,
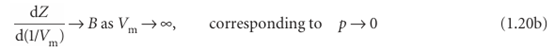
Because the virial coefficients depend on the temperature, there may be a tempera ture at which Z → 1 with zero slope at low pressure or high molar volume (Fig. 1.16). At this temperature, which is called the Boyle temperature, TB, the properties of the real gas do coincide with those of a perfect gas as p → 0. According to eqn 1.20b, Z has zero slope as p → 0 if B = 0, so we can conclude that B = 0 at the Boyle temperature. It then follows from eqn 1.19 that pVm ≈ RTB over a more extended range of pressures than at other temperatures because the first term after 1 (that is, B/Vm) in the virial equation is zero and C/V2m and higher terms are negligibly small. For helium TB =22.64 K; for air TB = 346.8 K; more values are given in Table 1.5.
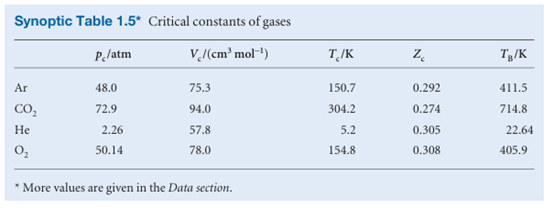
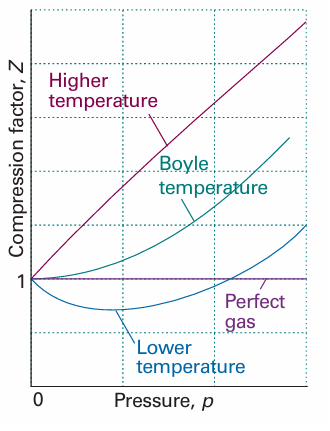
Fig. 1.16 The compression factor, Z, approaches 1 at low pressures, but does so with different slopes. For a perfect gas, the slope is zero, but real gases may have either positive or negative slopes, and the slope may vary with temperature. At the Boyle temperature, the slope is zero and the gas behaves perfectly over a wider range of conditions than at other temperatures.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
