لم يكن نيقولا سعدي كارنو أول من حاول أن يُوضّح إمكانية تحويل الطاقة الحرارية إلى عمل؛ فقد سبقه هيرون السكندري قبل ذلك، لكن كارنو قدم دراسة نظرية لمدى فعالية الآلة الحرارية البخارية، يُمكن تعميمها على تصميم أية آلة بخارية، وهو ما لم يفعله هيرون.

ففي عام 1824م قام بنشر كتاب صغير عن الآلة البخارية بعنوان «تأملات في القدرة المحركة للنار وفي الآلات التي تُعطي هذه القدرة» ⁹² وقدَّم في هذا الكتاب أدلته التي توضّح أن الطاقة الحرارية التي تتحول بوساطة آلة بخارية لا يمكنها أن تُنتِج إلا مقدارًا مُحَدَّدًا من العمل، ويعتمد هذا المقدار على الفرق في درجة الحرارة بين الجزأين الحار والبارد من الآلة، وفي حالة التوازن لا ينتج أي عمل بغَض النظر عن مقدار الحرارة التي تُنتجها. ⁹³

وقد أوجز كارنو في كتابه السابق ثلاثَ أوليَّات كانت بمثابة المعايير العامة التي يتم التحكُّم بها في مردود الآلة البخارية الفعالة وهي: ⁹⁴

(1) افتراضه بأنه يُمكن توليد عملٍ مُفيد كُلَّما وُجد فرق في درجة الحرارة.

(2) استخدامه نظرية السيَّال الحراري حتى يؤكّد إمكانية قياس كمية الحرارة التي تمتصها جملة فيزيائية أو تُصدرها لدى تفحص حالتي الجملة الابتدائية والنهائية.

(3) أكد أنَّ الحركة الدائمة مستحيلة، مع أنها كانت ترد في دراسة الميكانيك بما فيها بعض الدراسات التي قام بها والده شخصيًّا.

لكن كارنو أهمل التفاصيل المتعلقة بعمل الآلة، والتركيز على الجوانب الأساسية الآتية: ⁹⁵

(1) دخول الحرارة إلى الآلة الحرارية عند درجة مرتفعة نسبيًّا.

(2) تُحوّل الآلة جزءًا من هذه الحرارة إلى عمل.

(3) تلفظ الآلة ما تبقّى من الحرارة التي لم تتحول إلى عمل إلى الخارج، وذلك عند درجة حرارة مُنْخَفِضة نسبيًّا.

وقد كتب كارنو: «لطالما تساءل الناس عن القُوَّة المُحَرِّكة للحرارة هل هي قوة لا تنضب؟ وهل للتحسينات الممكن إدخالها على المحرّكات البخارية حد لا تسمح طبيعة الأشياء بتجاوزه بأية وسيلة، أم أنَّ في الوسع مواصلة هذه التحسينات إلى ما لا نهاية؟» ⁹⁶

لذلك انطلق كارنو في البحث عن إجاباته من نظرية السيال الحراري الشائعة والمنتشرة في الأوساط العلمية في عصره، وكان يتصوّر أنَّ السيَّال الحراري ينتقل بالفعل عبر الآلة فيُنتج عملا، تمامًا كالماء إذْ يُدير عجلات الطاحونة، ولم يُغيّر اعتقاده إلى أنَّ الحرارة هي وليدة الحركة إلا في أواخر أيَّامه، كما تبين ذلك من مذكراته. ⁹⁷

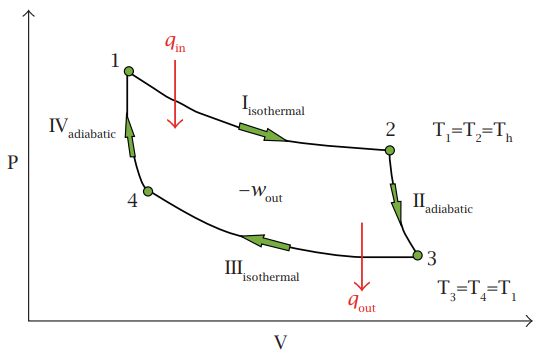
شكل بياني يوضّح دورة كارنو المثالية بين الضغط (P) والحجم (V)، فالتغير الإيزوثرمي من (1) إلى (2)، عند درجة حرارة T₁، ويتلوه تمدُّد أدياباتي ينتج عنه انخفاض في درجة الحرارة إلى T₂، والوصول إلى الحالة (3). ويسبب الضغط فالتغير الإيزوثرمي من (3) إلى (4)، عند درجة حرارة T₃، إلى الحالة التي ينجم عن الانضغاط الأدياباتي التالي ارتفاع درجة الحرارة إلى T₄ والعودة للحالة الأصلية (مصدر الشكل: https://chem.libretexts.org/Core).

ثمة فكرةً أخرى استحدثها كارنو وهي العملية الدورية التي تحمل اسمه (دورة كارنو) التي أرست أسس القانون الثاني في الثرموديناميك؛ فقد افترض في هذه الدورة التخيلية إمكانية انعكاس كل العمليات الداخلة فيها. ولتحقيق ذلك لا بد من أن تتكون الدورة من تسلسل لحالات التوازن؛ ومن ثَم تحدث بطريقة متناهية في البطء. هذه الدورة تتكون من تغيرين أيزوثرميين (أي ثابتي درجة الحرارة) في حجم كمية معزولة من الغاز، وتغيرين أديابتيين (أي بدون تبادل للحرارة مع الوسط الخارجي)، وقد مثلها الفيزيائي الفرنسي إميل كلابيرون E. Clapeyron (1799 – 1864م) بيانيا على شكل علاقة بين الحجم (v) والضغط (P). حيث استخدم كلابيرون منحني العلاقة بين الحجم والضغط ورموز حسابات التفاضل والتكامل لوضع أفكار كارنو بشكل عام يمكن استخدامه كأساس لنظرية محدودة ومُحكمة عن الحرارة، ولا يُعتقد أنه استولى على اختراع جون ساذرن ⁹⁹ J. Sazern ليبدأ إنتاج الآلات البخارية.¹⁰⁰

الهدف الذي كان يتوخاه كارنو من بحثه هو الجانب الصناعي والاقتصادي؛ فقد كانت الآلات البخارية المنتشرة في ذلك الوقت تستهلك وقودًا حتى تنجز عملها، فأراد أن يعرف مقدار العمل الذي تقوم به الآلة مُقابل حرق مقدارٍ مُحَدَّد من الوقود، وكيف يُمكِن زيادة مقدار هذا العمل مع بقاء مقدار الوقود ثابتًا. ¹⁰¹

_________________________________________

هوامش

92- Réflexions sur la puissance motrice du feu et sur les machines propres à developer cette puissance

93- أسيموف، إسحاق، أفكار العلم العظيمة، ص 85.

94- موتز، لويد وويفر، جيفرسون هين، قصة الفيزياء، ص 169.

95- سويلم، محمد عطية وآخرون، الفيزياء العامة، ص 348.

96- ويلسون ميتشل الطاقة، ص 57.

97- فوربس، ر. ج.، وديكستر، إ. ج.، تاريخ العلم والتكنولوجيا، ج2، ص 50.

98- المرجع السابق نفسه، ص 51-52.

99- كان واط إنسانًا عمليًّا، وكانت إحدى المشكلات العملية التي تواجهه هي كيفية تطابق القدرة الناتجة من آلة بخارية معيَّنة مع متطلبات القدرة في الماكينة التي تُديرها الآلة البخارية. وعندما وجد أحد المهندسين – الذي في خدمته – واسمه جون ساذرن طريقة لقياس مخرج القدرة، أيقن واط الميزة التي تمنحها هذه الطريقة فاحتفظ بالطريقة سرًّا. انظر: كوب كاتي ووايت هارولد جولد، إبداعات النار، ص 235.

100- كوب، كاتي ووايت، هارولد جولد، إبداعات النار، ص 235.

101- مطلب، محمد عبد اللطيف، تأريخ علوم الطبيعة، ص258.

102- موتز لويد وويفر جيفرسون هين قصة الفيزياء، ط 1، ص 170.

مواضيع ذات صلة

الاهتمامات البيئية العالمية "فيزياء الطاقة المستدامة: استجابة علمية للاهتمامات البيئية العالمية"

سلوك الغازات وخصائصها العامة

الديناميكا الحرارية الجزيئية

توزيع بولتزمان

العلاقات بين الخواص

القانون الثالث للديناميكا الحرارية

الطاقة الحرة

القانون الثاني للديناميكا الحرارية

القانون الأول للديناميكا الحرارية

Order and entropy

Irreversibility

The Clausius-Clapeyron equation