A root-finding method which was among the most popular methods for finding roots of univariate polynomials in the 19th and 20th centuries. It was invented independently by Graeffe, Dandelin, and Lobachevsky (Householder 1959, Malajovich and Zubelli 2001). Graeffe's method has a number of drawbacks, among which are that its usual formulation leads to exponents exceeding the maximum allowed by floating-point arithmetic and also that it can map well-conditioned polynomials into ill-conditioned ones. However, these limitations are avoided in an efficient implementation by Malajovich and Zubelli (2001).

The method proceeds by multiplying a polynomial 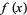 by 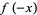 and noting that

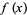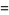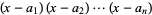			(1)
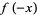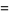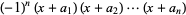			(2)

so the result is

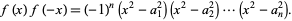(3)

repeat  times, then write this in the form

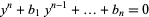(4)

where 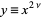. Since the coefficients are given by Vieta's formulas

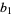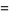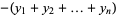			(5)
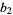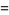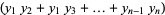			(6)
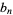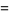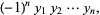			(7)

and since the squaring procedure has separated the roots, the first term is larger than rest. Therefore,

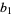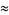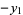			(8)
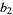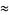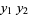			(9)
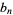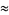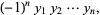			(10)

giving

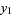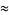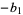			(11)
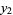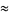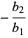			(12)
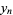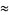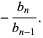			(13)

Solving for the original roots gives

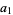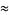		{-, {b, _, 1}}, {2, nu}]" src="https://mathworld.wolfram.com/images/equations/GraeffesMethod/Inline40.gif" style="height:27px; width:45px" />	(14)
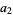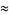		{-, {{(, {b, _, 2}, )}, /, {(, {b, _, 1}, )}}}, {2, nu}]" src="https://mathworld.wolfram.com/images/equations/GraeffesMethod/Inline43.gif" style="height:58px; width:50px" />	(15)
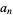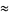		{-, {{(, {b, _, n}, )}, /, {(, {b, _, {(, {n, -, 1}, )}}, )}}}, {2, nu}]." src="https://mathworld.wolfram.com/images/equations/GraeffesMethod/Inline46.gif" style="height:58px; width:65px" />	(16)

This method works especially well if all roots are real.

REFERENCES:

Bini, D. and Pan, V. Y. "Graeffe's, Chebyshev-Like, and Cardinal's Processes for Splitting a Polynomial Into Factors." J. Complexity 12, 492-511, 1996.

Brodetsky, S. and Smeal, G. "on Graeffe's Method for Complex Roots of Algebraic Equations." Proc. Cambridge Philos. Soc. 22, 83-87, 1924.

Cajori, F. "The Dandelin-Gräffe Method." A History of Mathematics, 5th ed. New York: Chelsea, p. 364, 1962.

Dedieu, J.-P. "À Propos de la méthode de Dandelin-Graeffe." C. R. Acad. Sci. Paris Sér. I Math 309, 1019-1022, 1989.

Grau, A. A. "On the Reduction of Number Range in the Use of the Graeffe Process." J. Assoc. Comput. Mach. 10, 538-544, 1963.

Householder, A. S. "Dandelin, Lobačevskiĭ, or Graeffe?" Amer. Math. Monthly 66, 464-466, 1959.

Jana, P. and Sinha, B. "Fast Parallel Algorithms for Graeffe's Root Squaring." Comput. Math. Appl. 35, 71-80, 1998.

Kármán, T. Von and Biot, M. a. "Squaring the Roots (Graeffe's Method)." §5.8.C in Mathematical Methods in Engineering: An Introduction to the Mathematical Treatment of Engineering Problems. New York: Mcgraw-Hill, pp. 194-196, 1940.

Malajovich, G. and Zubelli, J. P. "Tangent Graeffe Iteration." 27 Aug 1999. http://arxiv.org/abs/math.AG/9908150.

Malajovich, G. and Zubelli, J. P. "On the Geometry of Graeffe Iteration." J. Complexity 17, 541-573, 2001.

Ostrowski, A. "Recherches sur la méthode de Graeffe et les zéros des polynomes et des séries de Laurent." Acta Math. 72, 99-155, 1940.

Ostrowski, A. "Recherches sur la méthode de Graeffe et les zéros des polynomes et des séries de Laurent. Chapitres III et IV." Acta Math. 72, 157-257, 1940.

Pan, V. Y. "Solving a Polynomial Equation: Some History and Recent Progress." SIAM Rev. 39, 187-220, 1997.

Runge, C. "The Dandelin-Gräffe Method." In Praxis der Gleichungen. Berlin and Leipzig, Germany: de Gruyter, pp. 136-158, 1921.

Whittaker, E. T. and Robinson, G. "The Root-Squaring Method of Dandelin, Lobachevsky, and Graeffe." §54 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 106-112, 1967.