A string figure is any pattern produced when a looped string is spanned between two hands and is twisted and woven in various manners around the fingers and the wrists. The combinations of crossings which can be realized in this way can be studied using knot theory.

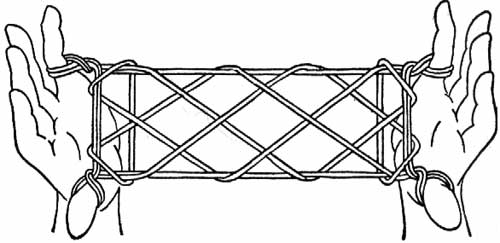
The string figure above is known as the Apache door (Jayne 1975, pp. 12-15, Fig. 21) or tent flap (Ball 1971, p. 5, Fig. 2).

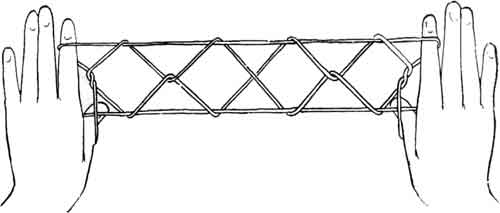
The string figure illustrated above is known as "Jacob's ladder," Osage diamonds (Jayne 1975, pp. 24-27, Fig. 50), the fishing net, or quadruple diamonds (Ball 1971, p. 19, Fig. 7).

String figures, which belong to the ancient traditions of many peoples around the world, and are even present in primitive cultures, are nowadays considered as a recreational activity in mathematics education. In English-speaking countries they are also known as the children's game called "cat's cradle."

REFERENCES:

Amir-Moéz, A. R. and Hamilton, J. D. "Art and Mathematics of String Figures." J. Recr. Math. 7, 23-34, 1974.

Amir-Moéz, A. R. String Figures: A Symbolic Approach. Lubbock, TX: Western Printing Company, 1979.

Ball, W. W. R. Ch. 16 in Mathematical Recreations and Essays, 5th ed. London: Macmillan, pp. 348-379, 1911. [The original Ch. 16 was removed in subsequent editions, and reprinted as a separate work by Ball (1928) and a collection of essays Ball et al. (1980).]

Ball, W. W. R. Fun with String Figures. New York: Dover, 1971.

Ball, W. W. R.; Petersen, J.; Carslaw, H. S.; and Cajori, F. String Figures and Other Monographs. New York: Chelsea, 1960.

Gibbs, W. and Sihlabela, M. "String Figures." Math. in School 25,24-27, 1996.

International String Figure Association. https://www.isfa.org/isfa.htm.

Jayne, C. F. String Figures and How to Make Them: A Study of Cat's-Cradle in Many Lands. New York: Dover, 1975.

Lee, E. "WWW Collection of Favorite String Figures." https://alysion.org/string.htm.

Probert, M. "String Figures, Mathematics, Origin." https://website.lineone.net/~m.p/sf/menu.html.

Scharringhausen, B. "String Figures." https://astrosun.tn.cornell.edu/~brs/strfigs/.