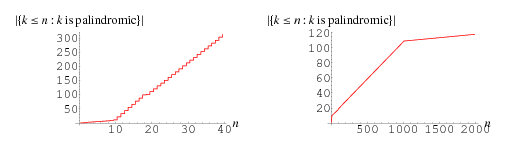
A palindromic number is a number (in some base 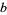) that is the same when written forwards or backwards, i.e., of the form 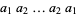. The first few palindromic numbers are therefore are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, ... (OEIS A002113). The number of palindromic numbers less than a given number are illustrated in the plot above.

A number 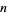 can be tested to see if it is palindromic in the Wolfram Language using PalindromeQ[n].

The numbers of palindromic numbers less than 10, 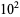, , 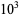... are 9, 18, 108, 198, 1098, 1998, 10998, ... (OEIS A050250). This sequence is given by the closed-form formula

{2(10^(n/2)-1) for n even; 11·10^((n-1)/2)-2 for n odd. " src="https://mathworld.wolfram.com/images/equations/PalindromicNumber/NumberedEquation1.gif" style="height:48px; width:214px" />

(1)

Banks et al. (2004) proved that almost all palindromes (in any base) are composite, with the precise statement being

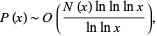(2)

where 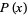 is the number of palindromic primes  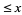and 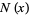 is the number of palindromic numbers .

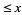The sum of the reciprocals of the palindromic numbers converges to a constant 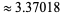 (OEIS A118031; Rivera), where the value has been computed using all palindromic numbers  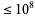is 3.370001832....

The first few 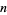 for which the pronic number  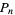is palindromic are 1, 2, 16, 77, 538, 1621, ... (OEIS A028336), and the first few palindromic numbers which are pronic are 2, 6, 272, 6006, 289982, ... (OEIS A028337). The first few numbers whose squares are palindromic are 1, 2, 3, 11, 22, 26, ... (OEIS A002778), and the first few palindromic squares are 1, 4, 9, 121, 484, 676, ... (OEIS A002779).

There are no palindromic square 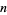-digit numbers for 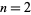, 4, 8, 10, 14, 18, 20, 24, 30, ... (OEIS A034822).

Numbers that are not the sum of two palindromes (where 0 is itself considered a palindrome) are 21, 32, 43, 54, 65, 76, 87, 98, 201, 1031, ... (OEIS A035137). Numbers that are not the difference of two palindromes are 1020, 1029, 1031, 1038, 1041, 1047, 1051, 1061, ... (OEIS A104444).

REFERENCES:

Banks, W. D.; Hart, D. N.; and Sakata, M. "Almost All Palindromes Are Composite." Preprint ESI 1456 (2004). Vienna, Austria: The Erwin Schrödinger International Institute for Mathematical Physics. Feb. 5, 2004. ftp://ftp.esi.ac.at:/pub/Preprints/esi1456.pdf.

Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematical Entertains. New York: Dover, 1964.

De Geest, P. "Palindromic Numbers and Other Recreational Topics." http://www.worldofnumbers.com/index.shtml.

De Geest, P. "Palindromic Products of Two Consecutive Integers." http://www.worldofnumbers.com/consec.htm.

De Geest, P. "Palindromic Squares." http://www.worldofnumbers.com/square.htm.

Dr. Pete. "The Math Forum. Ask Dr. Math: Questions & Answers from Our Archives. Palindromic Numbers." http://mathforum.org/dr.math/problems/akyildiz1.4.98.html.

Dr. Rob. "The Math Forum. Ask Dr. Math: Questions & Answers from Our Archives. Palindromic Numbers." http://mathforum.org/dr.math/problems/stang4.8.14.97.html.

Heinz, H. "Palindromes." http://www.magic-squares.net/palindromes.htm.

MathPages. "On General Palindromic Numbers." http://www.mathpages.com/home/kmath359.htm.

Pappas, T. "Numerical Palindromes." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 146, 1989.

Rivera, C. "Problems & Puzzles: Puzzle 056-The Honaker's Constant." http://www.primepuzzles.net/puzzles/puzz_056.htm.

Sloane, N. J. A. Sequences A002113/M0484, A002385/M0670, A002778/M0907, A002779/M3371, A028336, A028337, A034822, A035137, A050250, and A118031 in "The On-Line Encyclopedia of Integer Sequences."