Octagonal Heptagonal Number
المؤلف:
Sloane, N. J. A
المصدر:
Sequences A048904, A048905, and A048906 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
19-12-2020
1191
Octagonal Heptagonal Number
A number which is simultaneously octagonal and heptagonal. Let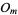 
denote the 
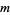th octagonal number and 
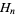the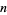 
th heptagonal number, then a number which is both octagonal and hexagonal satisfies the equation 
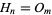, or
 |
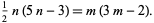(1)
|
Completing the square and rearranging gives
 |
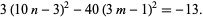(2)
|
Therefore, defining
gives the second-order Diophantine equation
 |
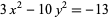(5)
|
The first few solutions are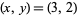 
, (7, 4), (73, 40), (157, 86), .... These give the integer solutions (1, 1), (345, 315), (166145, 151669), ... (OEIS A048904 and A048905), corresponding to the octagonal heptagonal numbers 1, 297045, 69010153345, ... (OEIS A048906).
REFERENCES:
Sloane, N. J. A. Sequences A048904, A048905, and A048906 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
